Forme trigonométrique d'un nombre complexe non nul

Nous avons vu que tout nombre complexe admettait une forme algébrique z = a + b.i

Donc tout nombre complexe peut être repérer dans le plan complexe.

Seuls les nombres complexes non nul peuvent cependant être étudiés pour leurs propriétés trigonométriques (en effet, comment former un angle avec 1 seul point ? )

Toute cette partie n'est valable que si le nombre nombre z est non nul, ce que l'on note :

On introduit Théta (en radian) et la longueur OM de cette manière :

Ainsi, dans le plan complexe, on obtient :

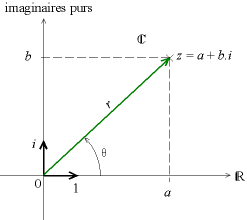
Vocabulaire :

1. Dans le plan complexe, on ne parle pas en terme "d'angles" mais on appelle cela les arguments.

==> UN argument du nombre complexe z, noté arg(z), est donc théta.

 Remarque :

On dit que z admet UN argument car une même position sur le cercle trigonométrique peut correspondre une infinité de points (ceux qui ont fait des tours entiers de cercle).

C'est la fameuse histoire du modulo 2pi présenté dans le rappel de trigonométrie.

Un argument (en radian) que forme un nombre complexe z non nul avec l'axe des abscisses est donc l'argument de z.

   2. La distance pour "atteindre" le nombre complexe z en partant l'origine du repère est la distance OM, qu'on appelle le module de z.

On écrit le module de z est noté |z|.

Sa valeur est : 

En effet, dans le triangle rectangle ci-dessous de côtés de longueurs "a" et "b", l'hypoténuse de ce triangle vaut d'après Pythagore sqrt(a^2+b^2) !

http://homeomath.imingo.net/module.htm

Remarques sur le module : 
- le module d'un nombre complexe est un réel positif.
- deux nombres complexes distincts peuvent avoir le même module.
 - le module d'un nombre réel est égal à sa valeur absolue, c'est pour cela qu'on conserve la notation avec les deux barres " | x | ".

De plus, on peut noter que :

La démonstration est extrêment simple :

Pour votre culture, je vous ai mis un tableau récapitulatif des notations utilisées dans les nombres complexes, ainsi que l'auteur et la date de chaque notation :

Tout nombre complexe peut se positionner dans le plan complexe.

Du coup, tout nombre complexe (non nul) peut se repérer dans le plan par son module et par un argument (mod 2pi).

Du coup, tout nombre complexe non nul peut s'écrire sous forme trigonométrique, c'est-à-dire :

Si existe deux situations dans laquelle la forme trigonométrique peut être écrite sous la forme algébrique.

• Cas 1 : si on connait la valeur du module |z|>0 et d'un argument de z, alors on peut tout simplement développer la formule précédente, ce qui donne : 

• Cas 2 si on ne connait que les valeurs de "a" et de "b", alors on a :

En effet,

Si deux points A et B d'affixes respectis z_A et z_B sont dans un repère orthonormé, alors :

La démonstration se fait logiquement ;

On est d'accord qu'il n'existe un unique point M qui vérifie :

Cependant, on sait que :

Or par définition,

Si deux points A et B d'affixes respectis z_A et z_B différentes sont dans un repère orthonormé, alors :

Démonstration :

Comme avant, on sait qu'il existe un unique point M tel que :

Comme nous l'avons démontré précédemment,

Si vous voulez comprendre la suite du cours et les techniques de calcul, il vous faudra avoir vu les propriétés de la fonction exponentielle que l'on voit en terminale.

Les propriétés de l'exponentielle sont semblables à ceux sur les puissance de nombres.

Il faudra donc vous renseigner sur la fonction exponentielle pour continuer la lecture sur les nombres complexes.

Vous pouvez toujours aller voir la rubrique "Fractales" si vous en l'avez pas encore fait ICI.

Sinon, continuons la lecture.

Un nombre complexe z de module |z| = 1 dont un argument est théta se note désormais :

Pour un angle théta donné, on a donc l'égalité :

Cette formule est à retenir par coeur; elle est FONDAMENTALE pour les nombres complexes.

Elle est très pratique car elle lie les propriétés de l'exponentielle et de la trigonométrie pour calculer les arguments des nombres complexes.

C'est d'ailleurs pour celà que cette notation est très utilisée.

C'est le mathématicien suisse Leonhard Euler qui l'a inventé.

Démontrons cette formule :

Rappels :

Sa formule se fait exactement de la même manière que celle de l'unicité de la fonction exponenetielle.

Tout nombre complexe de module 1 s'écrit sous la forme : 

Maintenant, posons la fonction f qui à tout réel théta, associe le nombre complexe :

L'idée est de démontrer que pour tous réels théta et théta', on obtient :

On remarque une ressemblance avec l'exponenetielle, non ?

Dérivons le produit des fonctions et comparons :

On obtient donc d'après les rappels :

De plus, on a que :

Ainsi, f transforme les sommes en produits et f(0) = 1, tout comme la fonction exponenetielle.

D'où l'idée de poser :

L'égalité que nous avons démontré auparavant peut donc aussi se noter :

Cette démonstration justifie le choix de la notation exponentielle.

Les démonstrations sont extrêmement simples :

Généralisation

On peut retenir e puissance << 2 kipi >> = 1

Les démonstrations prennent simplement en compte que le sinus et le cosinus sont 2pi-périodiques.

ATTENTION à l'écriture !!!

Il faut faire super attention aux parenthèses; en effet :

Finalement, tout nombre complexe non nul peut s'écrire sous la forme exponentielle :

Ainsi, tout nombre complexe se repère dans le plan de cette manière :

Remarque sur le conjugué d'une notation exponentielle :

La démonstration est rapide :

Voici les formules démontrées par Moivre :

La forme exponentielle et les propriétés de la fonction exponentielle vont beaucoup nous aider ici pour les démonstrations. La trigonométrie (2pi-périodique) va aussi nous aider !

1ère démonstration :

2ème démonstration :

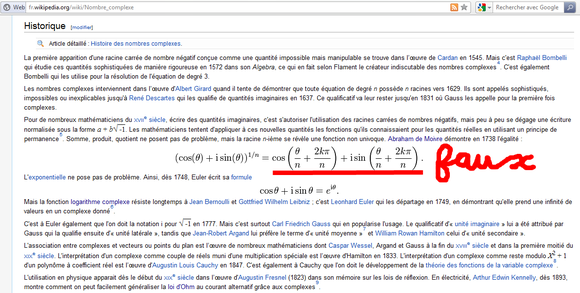
ATTENTION - En faisant ce sujet, j'ai découvert une énorme erreur sur Wikipédia.

C'EST ARCHI FAUX ! : (partie historique) http://fr.wikipedia.org/wiki/Nombre_complexe

Maintenant que nous savons ce qu'est un argument et le module d'un nombre complexe, alors nous pouvons maintenant analyser les propriétés sur le module et l'argument.

Pour cela, cliquez ICI.