A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
Rappels de trigonométrie (dans R)
1. Qu'est-ce-que la trigonométrie ?
La trigonométrie (du grec τρίγωνος / trígonos, « triangulaire », et μέτρον / métron, « mesure ») est une branche des mathématiques qui traite des relations entre distances et angles dans les triangles et des fonctions trigonométriques telles que sinus, cosinus et tangente.
2. De la trigonométrie dans les triangles rectangles
Hypoténuse, côté opposé et côté adjacent
Dans tout triangle rectangle, on retrouve :
1. L'hypoténuse : c'est le côté opposé à l'angle droit.
L'hypoténuse est le plus grand des côtés du triangle rectangle.
2. Le côté adjacent et le côté oppsé :
Si nous prenons l'angle (CAB) [avec un chapeau dessus], alors son côté adjacent est AB et son côté opposé est CB.
Pour l'angle (ACB) [avec un chapeau dessus], alors son côté adjacent est CB et son côté opposé est AB.
Voici un schéma complet :
Définition du cosinus, du sinus et de la tangente
Comme précisé en introduction, la trigonométrie premet de créer des relations entre les distances et les angles.
Grâce aux définitions qui vont suivre, on va pouvoir tisser des rapport entre les angles et les longueurs des côtes qui forment cet angle dans le triangle rectangle.
On définit le cosinus comme étant le rapport entre le côté adjacent à l'angle par rapport à l'hypothénuse.
Le sinus est le rapport entre le côté opposé à l'angle par rapport à l'hypothénuse.
Enfin, la tangente est le rapport entre le sinus et le cosinus, ce qui revient à faire le rapport entre le côté opposé à l'angle et le côté adjacent à l'angle.
Le schéma suivant illustre bien tout celà :
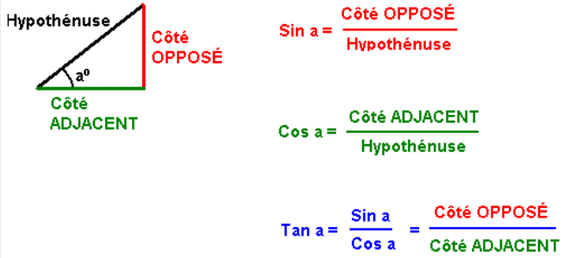
Moyen mnémotechnique 1 : SOH-CAH-TOA
SOH : Sinus = Opposé sur Hypoténuse ;
CAH : Cosinus = Adjacent sur Hypoténuse ;
TOA : Tangente = Opposé sur Adjacent.
Moyen mnémotechnique 2 (pas très sympa) : CAH-SOH-TOA
CAH : Cosinus = Adjacent sur Hypoténuse ;
SOH : Sinus = Opposé sur Hypoténuse ;
TOA : Tangente = Opposé sur Adjacent.
Angles à valeurs remarquables
Nous démontrerons ces résultats plus tard.
3. Extension au cercle trigonométrique
A la découverte du cercle unitaire
Un cercle trigonométrique est un cercle vérifiant 2 conditions :
--> c'est un cercle de rayon 1
--> c'est un cercle orienté auquel on a donné un sens direct, positif ou trigonométrique qui est orienté dans le sens contraire des aiguilles d'une montre et un sens indirect, négatif ou horaire qui est orienté comme dans le sens des aiguilles d'une montre.
Le sens direct est symbolisé par un une flèche et un "+" indiquant le sens d'orientation.
Par exemple, le cercle suivant est un cercle trigonométrique :
L'utilité d'un cercle trigonométrique est de modéliser des points se trouvant sur la périphérie du cercle.
On repère un point en fonction de sa position par rapport à l'axe des abscisses et des ordonnées.
La tangente à une courbe
Le mot tangente vient du latin tangere, toucher : en géométrie, la tangente à une courbe en un de ses points est une droite qui « touche » la courbe au plus près au voisinage de ce point. La courbe et sa tangente forment alors un angle nul en ce point.
La tangente à un cercle
Une tangente à un cercle est donc une droite qui coupe ce cercle en un unique point que l'on appelera I. La tangente à un cercle est la droite qui "frôle" ce cercle au point I.
La droite (OI) et la tangente à C sont perpendiculaires en un unique point I.
4. Une histoire de distance par correspondance : le radian
Qu'est-ce-que le radian ?
Le radian est une unité de mesure d'angles.
La mesure d'un angle orienté s'exprime généralement en radian.
Si on prend un cercle de rayon 1 sur lequel on colle un morceau de ficelle de longueur 1,
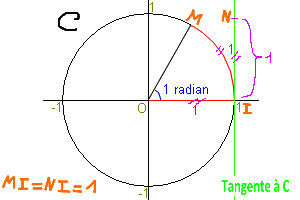
<<1 radian>> est la mesure de l'angle formé par le centre du cercle et les 2 extrémités de la ficelle. D'une manière générale un angle qui mesure x radians est obtenu avec un morceau de ficelle de longueur x.
La mesure initiale de la ficelle se fait sur la tangente à la courbe C à partir du point I (point d'intersection entre C et la tangente) et on reporte sa mesure sur le cercle en partant de I et en faisant le pourtour du cercle jusquà ne plus qu'avoir de bout de la ficelle.
==> il y a TOUJOURS égalité entre IN et IM : IN = IM.
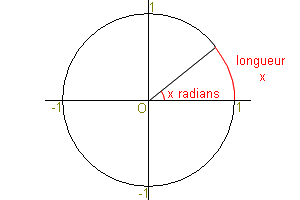
A une longueur donnée, on peut également associer un angle grâce au radian.
Il existe deux superbes animations qui simulent la situation d'enroulement de la corde sur le cercle :
http://matoumatheux.ac-rennes.fr/geom/trigonometrie/2/conv1.htm
Remarque :
Pour plus d'un tour de cercle (périmètre d'un cercle =2.pi.r = 2.pi.1 = 2.pi), on retombe sur un même point M.
Il existe donc une infinité de point en un même endroit du cercle car on peut faire des tours de cercles à l'infini.
On écrit alors :
Tableau de correspondace degré/radian :
Les degré doivent sûrement plus vous parler que les radian.
Il existe pour celà des tableau de correspondance entre les degrés et les radians.
A force de manipuler des mesures en radians, on s'y habitue assez rapidement.
Si vous retenez que 180° correspond à pi radian, alors si vous cherché la mesure d'un angle en radian ou en degré, il suffit juste de faire un simple produit en croix et le trou est joué !
Ainsi, un angle de 1 radian mesure exactement 180/pi degré, soit environ 57,3°.
Le tableau ci-dessus vous permet de passer des degré en radian (avec le produit en croix) :
5. La notion de cosinus et de sinus dans le cercle unitaire
Définition des termes
On choisi par convention l'axe des abscisses comme étant le cosinus et l'axe des ordonnées comme étant le sinus.
Tout point M sur le cercle trigonométrique peut donc se repérer selon son cosinus et son sinus.
M a donc pour coordonnées :
En fait, le triangle rectangle OMH est exatement le même que celui vu au début de ce rappel !
Propriétés fondamentales en trigonométrie
En regardant le cercle, celà est tout à fait normal et logique.
Un angle se trouvant sur la périphérie du cercle a forcément son abscisse, donc son cosinus qui est dans [-1;1], de même pour son sinus.
En effet, au bout d'un tour, on retourne sur le même point du cercle, possédant donc le même cosinus et le même sinus.
On dit que le cosinus et le sinus sont 2-pi périodiques.
La démonstration provient de Pythagore.
En effet, dans le triangle rectangle OMH (schéma du haut), on a :
Si vous voulez en savoir plus sur la trigonométrie, vous pouvez aller voir les liens suivants :
http://www.lyc-curie-sceaux.ac-versailles.fr/IMG/pdf/ftrigo.pdf
http://www.methodemaths.fr/cercle_trigo.php#duplication
http://gilles.costantini.pagesperso-orange.fr/Lycee_fichiers/CoursP_fichiers/trigo.pdf
6. Valeurs remarquables
Valeurs remarquables du cosinus :
http://matoumatheux.ac-rennes.fr/geom/trigonometrie/2/cerclecos.htm
Valeurs remarquables du sinus :
http://matoumatheux.ac-rennes.fr/geom/trigonometrie/2/cerclesin.htm
Voici un petit tableau récapitulatif :
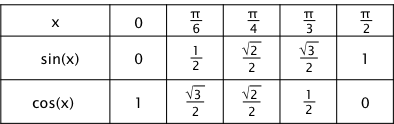
Voici également deux cercles avec les valeurs et les angles remarquables associés :
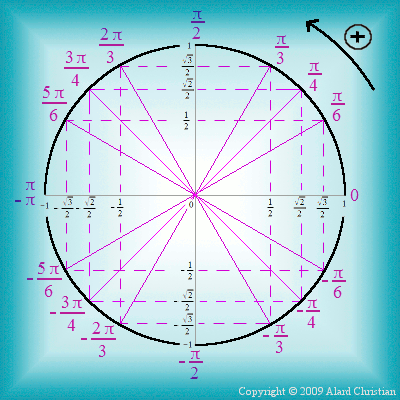
Démonstrations de ces résultats :
Vous pouvez aller voir ce pdf qui les démontre très bien de manière géométrique :
http://gilles.costantini.pagesperso-orange.fr/Lycee_fichiers/CoursP_fichiers/trigo.pdf
Sinon, vous pouvez utiliser la formule fondamentale de la trigonométrie pour les démonstrations :
Les deux techniques sont équivalentes.
Renseignez-vous sur Internet pour plus de détailles; l'objet de ce site est de faire découvrir les nombres complexes et non la trigonométrie pure.
On en a certes bien besoin pour les complexes, mais il faut surtout comprendre ce qu'est le radian et connaître les propriétés ci-dessus.
Mais la trigonométrie reste néanmoins un sujet tout à fait intéressant !
Nous pourrez par exemple démontrer que :
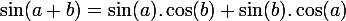
Maintenant que nous avons fait ces rappels, nous pouvons passer à la trigonométrie complexe.
Pour cela, cliquez ICI.
