Représentation géométrique d'un nombre complexe
Un nouveau plan - le plan complexe :
Les complexes ne servent pas uniquement à faire des calculs algébriques, on peut également les repérer dans un nouveau repère complexe :
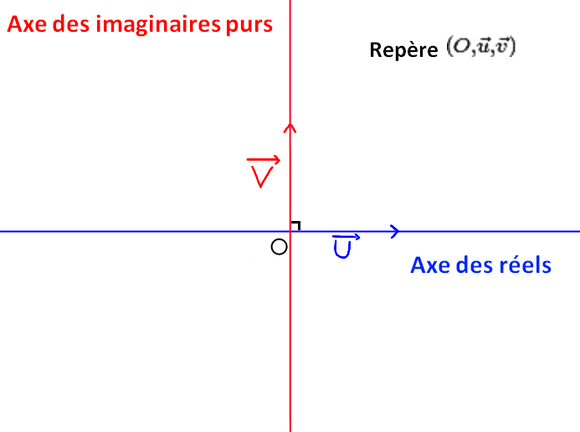
Remarque :
http://paquito.amposta.free.fr/glosso/orthonor.htm
Les termes "orthonormé","orthonormal" et "orthogonal" ont des sens différents.
Orthogonal signifique qu'il y a un angle droit.
==> ("ortho" = droit)
Orthonormé ou Orthonormal signifie qu'il y a un angle droit ET que les normes/distances sont égales à 1
==> le repère est formé par deux vecteurs unitaires orthogonaux.
==> ("ortho" + "norme")


Un repère quelconque est un repère qui n'est ni "orthonormé/orthonormal" ou "orthogonal" (mais il PEUT vérifier une des caractéristiques : en effet, les repères "orthonormé","orthonormal" et "orthogonal" sont en fait des repères quelconques "améliorés").
Voici un résumé :

La notion d'affixe d'un point :
Définition
Tout nombre complexe peut s'écrire sous une forme algébrique z = a +b.i
Du coup, un point M quelconque peux donc se repérer dans le plan complexe car il possède une partie réelle "a" et une partie imaginaire "b".
M a par conséquant comme coordonnées :

Cependant on peut aussi repérer directement M grâce à sa forme algébrique.
On peut donc écrire M de cette manière :

On dit que M a pour affixe z = a + b.i
Ainsi, un point M de coordonnées M( a;b ) est le point ayant pour affixe z = a+b.i, que l'on note M( z = a+b.i ) ou M ( a+b.i ) ou M(z).
Conséquences graphiques
Si M appratient à l'axe des abscisses (= axe des réels), alors Im(z) = 0.
Si M appartient à l'axe des ordonnées (= axe des imaginaires purs), alors Re(z) = 0.

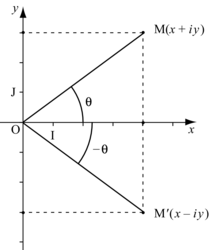
Deux nombres complexes conjugués sont symétriques par rapport à l'axe des abscisses.
En effet, les parties imaginaires étant opposées et leurs parties réelles restant identique, celà semble logique.
Illustrons cela :
La notion d'affixe d'un vecteur :
Affixe d'un vecteur :
De manière analogue, tout vecteur peut se repérer par ses coordonnées ou bien par son affixe.

Affixe d'un vecteur formé par deux points M et M' :
Tout vecteur formé par deux points M ( z_{M} ) et M' ( z_{M'} ) quelconques admet pour affixe :

La démonstration se base en fait sur les coordonnées de ce vecteur :


En transformant les coordonnées de ce vecteur en affixe, on obtient :

Régles de calcul sur les affixes :

Si deux vecteurs sont égaux, alors ils ont les mêmes affixes.
Si deux vecteurs ont la même affixe, alors ils sont égaux.
On note alors :

Le vecteur formé par la somme de deux vecteurs a pour affixe la somme des affixes des deux vecteurs. On a :

On retrouve la même relation de Chasles que dans R.
De la même manière :

Un même vecteur aditionné "k" fois aura donc pour affixe :

Soit le segment [AB].
Le milieu S de [AB] a comme affixe :

Voici une super animation qui montre la manière de se repérer dans le plan complexe et les propriétés qui en surgissent :
Je vous propose ensuite de voir la forme trigonométrique d'un nombre complexe non nul en cliquant ICI.
Remarque IMPORTANTE:
Si vous avez du mal ou que vous ne connaissait pas ce qu'est la trigonométrique, alors un rappel est fait ICI.
 A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?