A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
L'ensemble de Mandelbrot, une fractale construite par une relation de récurrence, liant des nombres complexes entres-eux
Modélisation
Il existe plusieurs types de fractales, mais une grande famille réunit celles qui sont définies par une relation de récurrence définissant une suite. C’est notamment le cas de l’ensemble très célèbre sur lequel travailla le mathématicien Benoît Mandelbrot.
Cet "ensemble de Mandelbrot" est défini par la suite :
Ici, "c" est une constante complexe qui balaye le plan complexe et "z" est une variable également complexe.
Au fur et à mesure que la récurrence progresse, l'ensemble de Mandelbrot se forme :
Résolution
On calcule chaque terme de la suite itérative ( en sachant que : z_0 = 0 ).
L’itération permet d’obtenir une série de nombres complexes :
La liste des z_0, z_1, z_2... générée par cette itération s’appelle l’orbite de z_0 sous l’itération de z_2 + c.
Il est donc nécessaire de se pencher sur la limite de ces orbites : est-ce que les orbites divergent ou convergent ? Sont-elles cycliques ou bien se comportent-elles de façon irrégulière ?
Prenons quelques exemples avec comme point initial constant z_0 = 0. On a construit le tableau récapitulatif suivant :
Comme on peut le voir dans le tableau, il y a des points dont l’orbite tend vers l’infini, c’est-à-dire des points pour lesquels la suite {z_n} diverge, ce qui est appréciable dès que la norme |zn| est supérieure à 2.
Ces points n’appartiennent donc pas à l’ensemble de Mandelbrot.
Inversement, il y a des points dont l’orbite est soit fixe, soit cyclique entre des valeurs dont la norme est inférieure à 2, et dans ces cas-là, les points appartiennent à l’ensemble.
Il est cependant difficile de conclure qu’un point n’appartient pas à l’ensemble. Si on observe que le module |z_n| <= 2 pour n variant de 0 à 30, alors on conclut qu’il est probable que le point n’appartienne pas à l’ensemble de Mandelbrot .
En théorie on devrait laisser n aller jusqu’à l’infini, mais c’est impossible en pratique.
A voir également
http://villemin.gerard.free.fr/Wwwgvmm/Suite/FracComp.htm#Top
https://deptinfo-ensip.univ-poitiers.fr/FILES/TPS/FRACTALES/suites.php
A la recherche des points invariants pour dessiner le squelette de l'ensemble de Mandelbrot
On peut chercher les points périodiques de l'ensemble de Mandelbrot avec cherchant à résoudre les équations de compositions du polynôme :
A savoir :
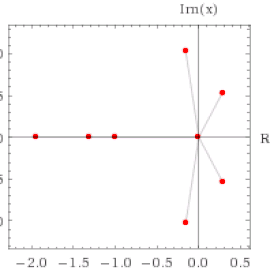
* les points de période 3 sont donnés en cherchant les solutions de :
Si on trace les racines complexes (2^2=4 au total, ce qui correspond au degré de ce polynôme d'après le théorème de D'Alemberg) dans le plan complexe, on obtient grâce à WolframAlpha:
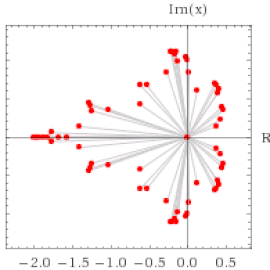
Plus on cherche des points de période élevée, plus le squelette de notre fractale va se dessiner.
Le profil de l'ensemble de Mandelbrot commence à se former au fur et à mesure que les points périodiques sont trouvés.
Mais bon, pour trouver par exemple les pour les points de période 7, il faut chercher les 64 racines complexes d'un polynôme de degré 64 ! C'est beaucoup quand même !!!
Heureusement que l'ordinateur est là pour nous résoudre et nous placer ces points dans le plan, sinon, c'est l'horreur.
Par ailleurs, si on regarde le graphe du polynôme donnant les points de période 7, on se rend compte que ces racines réelles (indiquées en rouge) sont comprises dans l'intervalle ]-2;1[ :
Je vous propose désormais de découvrir un logiciel de simulation fractale XaoS.
Pour cela, cliquez ICI.
