Propriétés sur le module et l'argument
1. Propriétés sur le module :
Rappel

On rappelle que le module est synonyme de distance.
Sa formule pour les nombres complexes z et z' est :

Cette valeur est issu d'un triangle rectangle de côtés de longueurs "a" et "b".
La mesure de son hypoténuse vaut alors de longueur sqrt( a^2 + b^2 ) d'après Pythagore.

Remarques :
--> le module d'un nombre complexe est un nombre réel positif.
--> deux nombres complexes distincts peuvent avoir le même module.
--> le module d'un nombre réel est égal à sa valeur absolue, c'est pour cela qu'on conserve la
notation avec les deux barres " | x | ".
Propriétés sur les modules similaires
Si un module est nul, alors le nombre complexe est tout simplement le complexe z = 0.
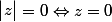
La démonstration est express :

Le module de z, z barre, -z et -z barre est de même valeur.
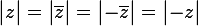
La démonstration est simple :




De façon géométrique, c'est d'autant plus visible :
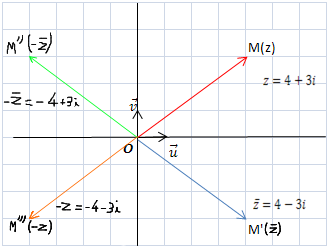
Il y a 2 symétrie axiales et 1 symétrie centrale par rapport au point M(z).
Le produit de z et se son conjugué z barre
Le produit de z et de son conjugué z barre est égal au module de z au carré.

Démonstration :


Remarque :
On aurait aussi pu l'écrire, d'après ce que nous venons de démontrer en haut :
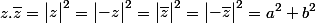
Le module du produit est le produit des modules
Le module de z multiplié par z' est égal au module de z multiplié par le module de z'.

Démonstration :
On sait que :

Donc on a que :

Ainsi, on a que :

En passant par la racine carrée, on obtient :

Le module de la puissance est la puissance du module
Le module de la puissance de z est égal à la puissance du module de z.
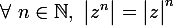
La démonstration se fait par récurrence :

Le module de l'inverse est l'inverse du module
Le module de l'inverse de z est égal à l'inverse du module de z.
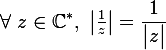
Le démonstration se fait assez stratégiquement :

Remarque :
Vous voyez bien ici que la valeur absolue et les modules sont représentés par un même symbole pour les nombres réels.
Ce n'est pas par hasard : le module d'un nombre réel est égal à sa valeur absolue, c'est pour cela qu'on conserve la notation avec les deux barres " | x | ".
Ainsi, on a établi que :

Le module du quotient est le quotient des modules
Le module de z par rapport à z' est égale au module de z par rapport au module de z'.
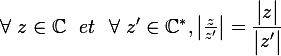
Le principe de la démonstration est le même que précédemment :

L'inégalité triangulaire des modules
Le module de z + z' est inférieur ou égal au module de z + le module de z'.

Démonstration :
http://mathsprepa.free.fr/Mathsprepa0607/Cours/Chap/C01.pdf
Remarque :
Il y a égalité lorsque la condition suivante est respectée :
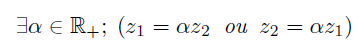
En effet, avec cette condition, z_1 est aligné avec z_2 et z_1 <= z_2 afin de cumuler les distances sans qu'elles ne se simplifient.
2. Propriétés sur l'argument :
Rappels

Cependant, notre triangle rectangle est celui-ci :
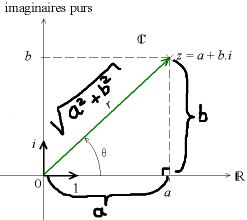
Donc du coup :

Pour toute la suite des propriétés, on définira toujours :

ATTENTION :
En effet, il est SUPER important que les nombres complexes soient non nuls car l'argument de zéro n'existe pas !
En voici la preuve :

Comme la division par zéro est impossible, alors arg(0) n'existe donc pas !
Propriétés sur les arguments similaires



Ce schéma illustre tout celà :
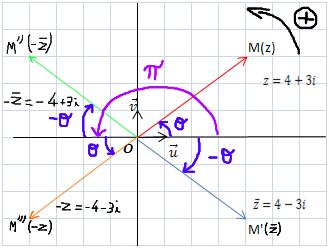
Si on se visualise bien la situation, on n'a même pas besoin de les apprendre.
L'argument du produit est la SOMME des arguments
L'argument de z.z' est égale à la SOMME des arguments de z ' et z'.

La démonstration est un peu technique, mais bon.
On suppose vrai ces prérequis :


De plus, on introduit :

Le produit de z.z' vaut alors : (mod 2.pi)



Ainsi, on obtient :

La formule de Moivre
L'argument de z^n est égale à "n" fois l'argument de z.

La démonstration se fait très rapidement par récurrence :

L'argument de l'inverse est égale à l'OPPOSE de l'argument
L'argument de l'inverse de z est égal à l'opposé de l'argument de z.

La démostration est un peu technique mais pas dure :

Mais on sait également que :

Ainsi, on peut former une égalité qui donne lieu à :

L'argument du quotient est égal à la DIFFERENCE des arguments
L'argument de z par rapport à z' est égal à l'argument de z moins l'argument de z'.

On démontre ce résultat de la même manière que précédemment :

Remarque :
On retrouve les propriétés semblables à celles du logarithme !
Voici une vidéo qui approfondie tout ce que nous venons de voir :
Maintenant que nous connaissons bien tout cela, nous pouvons enfin passer aux transformations complexes dans le plan en cliquant ICI.
 A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?



