PAR JOSIANE LAJOIE (JUIN 2006)
Voici les grandes étapes pour que les fractales puissent apparaître et se développer :


Au IVe siècle avant J.-C. : Euclide définit la notion de dimension entière
OBJETS DE LA GÉOMÉTRIE EUCLIDIENNE
http://www.sciences.ch/htmlfr/geometrie/geometrieeuclidienne01.php
D1. La notion expérimentale la plus simple est celle de "volume". Nous disons qu'un corps occupe un certain volume lorsqu'il occupe dans l'espace à trois dimensions une certaine place (pour des
espaces à des dimensions supérieures, nous parlons d'hyper-volumes).
D2. Nous admettrons comme une chose évidente qu'un volume est limité par une "surface"; mais si l'existence du volume est physiquement contrôlable et mesurable, la surface est une création de
l'esprit; c'est quelque chose d'analogue à une baudruche, par exemple, enveloppant un volume quelconque, mais d'analogue seulement. C'est un être géométrique à deux dimensions sans
épaisseur.
D3. Lorsqu'une surface est limitée, cette limite est une "ligne". Ici encore, la ligne est une création de l'esprit, une ligne n'a pas d'existence expérimentale; c'est quelque chose d'analogue à
la figure formée par un fil de fer. Etre géométrique encore mais d'une dimension sans hauteur ni largeur.
D4. Une "droite" est définie comme la ligne de plus court chemin joignant deux points sur une surface.
D5. Quand une ligne est limitée, sa limite est un "point": le point est quelque chose d'analogue à l'intersection de deux fils tendus. C'est encore une création de l'esprit, un être géométrique.
D6. L'expression le "segment" AB désigne en général une ligne limitée par les points A et B.
D7. Nous appelons "angle" (ou "angle plan") ou plus rigoureusement "angle rectiligne" la portion de plan limitée par deux demi-droites.
DIMENSIONS
Dans la "dimension topologique", le point (abstraction mathématique et géométrique) a une dimension topologique de 0, la courbe (trait continu d'épaisseur nulle) une dimension de 1, la surface une dimension de 2, un volume une dimension de 3 et un hyper-volume une dimension 4 (pour représenter un hyper-volume, prenez un volume dessiné sur papier (...) et faites-en une translation et reliez les sommets).
Ce sont toutes des valeurs entières par définition :
Au IIIe siècle avant J.-C., Apollonius construit la première Fractale grâce à sa baderne d'apollonius
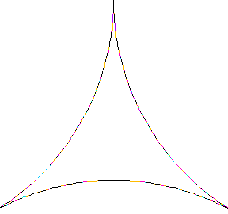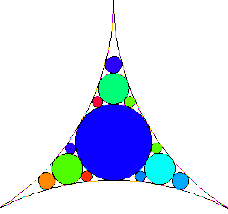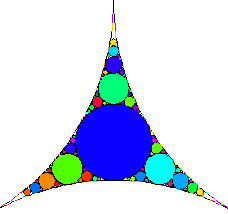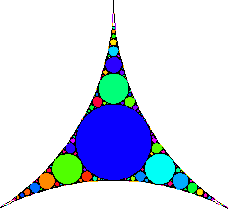
La baderne d’Apollonius est le plus ancien exemple de fractale, datant d’Apollonius de Perge, IIIème siècle avant J.C. célèbre pour ses écrits sur les sections coniques.
(C'est lui qui donna à l'ellipse, à la parabole et à l'hyperbole les noms que nous leur connaissons.)
On part d’un triangle curviligne dont les côtés sont des arcs de cercle. On y inscrit un cercle, tangent aux trois côtés. Puis on construit des cercles, tangents aux côtés et au cercle. On
recommence la construction indéfiniment.

En mathématiques, les cercles d'Apollonius forment une figure de géométrie fractale engendrée à partir de trois cercles, deux quelconques d'entre eux étant tangents à un troisième. Ils ont été nommés ainsi en l'honneur du mathématicien grec Apollonios de Perga.
La construction des cercles d'Apollonius possède une dimension de Hausdorff égale à 1,3057
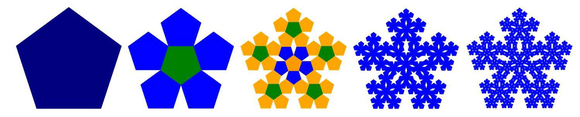
Au XVIe siècle, le peintre Dürer introduit les Pentagones fractals, appelés "Pentaflake"
http://www.3dfractals.com/docs/Master_Thesis_Lajoie.pdf
Le peintre allemand Albretch Dürer, inspiré par Léonard de Vinci, croyait que les arts
devaient être basés sur les sciences en particulier sur les mathématiques qui, selon lui,
étaient la branche des sciences la plus exacte, la plus logique et la plus efficace d’un
point de vue graphique.
Son image fractale consiste en un pentagone régulier dans lequel on place six petits pentagones congrus ; cinq d’entre eux doivent recouvrir les angles du pentagone initial de façon à ce que les côtés adjacents correspondent et le dernier pentagone doit se situer au centre du grand pentagone mais en ayant subi une rotation de 180° par rapport à celui-ci.
Le mot Pentaflake est formé du préfixe "penta-" = 5 côtés et du suffixe "flake" = flocon en anglais.
Si vous voulez plus d'information sur le Pentaflake, allez voir ces liens :
http://mathworld.wolfram.com/Pentaflake.html
http://villemin.gerard.free.fr/Wwwgvmm/Suite/FracDure.htm
http://ecademy.agnesscott.edu/~lriddle/ifs/pentagon/Durer.htm
AU XVIIIe siècle, Leibniz introduit la notion d'autosimilarité
L'autosimilarité est le caractère d'un objet dans laquelle on peut trouver des similarités en l'observant à différentes échelles.
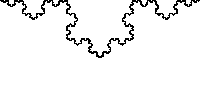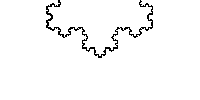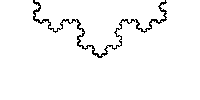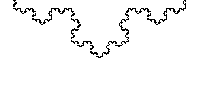

En 1830, Bolzano invente la toute première courbe partout continue et nulle part dérivable
http://eljjdx.canalblog.com/archives/2009/06/28/14224286.html
La toute première courbe partout continue et nulle part dérivable est l'œuvre du mathématicien tchèque Bernard Bolzano, découverte en 1830. Il faudra tout de même attendre 1930 avant qu'elle ne soit publiée. Par sa construction, on peut l'identifier comme étant la première fractale de l'histoire !
http://mp.cpgedupuydelome.fr/document.php?doc=Article%20-%20Epaisseur%20de%20la%20continuit%E9.txt
Pour représenter la fonction de Bolzano, on part d'un segment joignant l'origine au point de coordonnées (1,1) du plan (étape 0). On le coupe en trois segments égaux, on fixe les
extrémités initiales et on double la pente des deux segments extrêmes, enfin, on transforme le segment intermédiaire de sorte de maintenir la continuité (étape 1). On applique de nouveau le
mécanisme précédent à chacun des trois segments de cette ligne brisée (étape 2) et on recommence à l'infini. Chaque ligne brisée obtenue est la courbe représentative d'une fonction réelle
continue définie sur le segment [0,1]. On peut montrer que cette suite de fonctions
converge uniformément, la fonction limite est appelée fonction de Bolzano.
La fonction de Bolzano est continue mais dérivable en aucun point car les pentes des segments des lignes brisées intermédiaires tendent vers l'infini. Le graphe d'une telle fonction fait penser à
un mouvement brownien, c'est à dire un mouvement changeant de direction à chaque instant.
Elle ressemble à ceci :
Après un très grand nombre d'itérations, on obtient donc la courbe de Bolzano :
En 1872, Weierstrass créé un autre exemple de fonction dont la courbe est continue mais non dérivable
Le mathématicien Weierstrass a créé une fonction f qui est continue mais dérivable en aucun point de sa courbe représentative.
Voici la formule de cette fonction :
Choisir 0 < a < 1, b entier impair distinct de 1 et ab > 6 (plus précisément si ab > 1 + 3p/2).

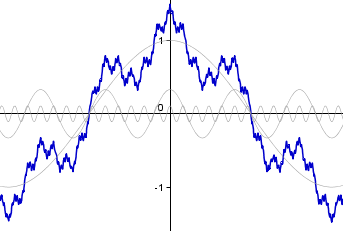
Représentation de la fonction de Weierstrass sur l'intervalle [-2,2].
La fonction a un comportement fractal; n'importe quel zoom (par exemple le cercle rouge) ressemble au zoom total.
Augmentation linéaire de la valeur de b de 0.1 à 5
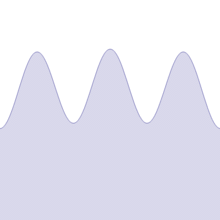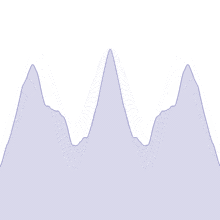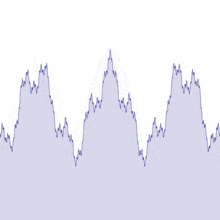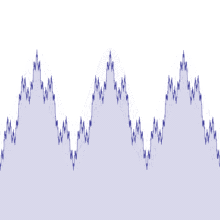
On peut donc dire dans les cas de Bolzano et de Weierstrass, la somme de fonctions dérivables à permi d'obtenir une fonction continue et non dérivable !
En 1883, Cantor publie son ensemble triadique, aussi appelé "poussière de Cantor"
Pour construire l’ensemble triadique de Cantor, il faut prendre l’intervalle [0, 1] que l'on divise en trois parties égales. A chaque itération, il faut retirer le tiers central, ce qui conserve les extrêmités de cet ensemble.
Ensuite, il faut enlever le tiers central de chacun des nouveaux segments obtenus et répéter ce processus indéfiniment.
Celà nous donne alors :
On parle bien de poussière de Cantor car à la n-ième étape, la suite semble former des segments de longueur aussi fin que des gains de poussière.
Chaque étape est en fait constituée de 2^n intervalles mis en union.




Remarque :
Pour former à la main ces réunions d'intervalles fermés, c'est assez monstrueux à première vue car il ne faut pas oublier d'enlever ce qui a été supprimé lors des dernières itérations.
J'ai trouvé une technique pour contourner ce problème :
A chaque fois que la fraction se simplifient (ex : 3/27 = 1/9 ou encore 9/27 = 1/3), la borne de l'intervalle suivant aura le même dénominateur avec le même numérateur augmenté de 1.
En 1890-91, de nouveaux exemples apparaîssent avec les courbes de Peano et de Hilbert
A la fin du XIXe siècle, Peano et Hilbert ont construit presque simultanément une courbe qui remplit un carré.
La courbe de Peano (1890)
http://www.bibmath.net/dico/index.php?action=affiche&quoi=./p/peano.html
Il est bien connu, en géométrie, qu'un point est de dimension 0, et qu'une courbe, c'est de dimension 1, ça ne peut jamais remplir tout l'espace! Et bien, détrompez-vous! Le mathématicien italien Giuseppe Peano a construit en 1890 une courbe qui remplit tout le carré, sans jamais se recouper. Voyons comment faire : on partage un carré en 9 petits carrés égaux, et on exécute le dessin suivant :
Ce dessin sera le motif de base. Partageons maintenant toujours notre carré en 9, mais dans chaque petit carré, on trace le motif de base, que l'on peut tourner de sorte que l'on fasse un chemin continu.
Et on répète ainsi l'opération. La courbe obtenue après une infinité d'opération est la courbe de Péano.
Cette courbe est c'est une fractale, qui se caractérise notamment par son autosimilarité lors du remplissage du carré.
La courbe de Hilbert (1891)
Quelques années après Peano, en 1891, Hilbert en a donné une variante à la courbe de Peano dont voici les premiers motifs :
Les courbes de Moore (1900)
En 1900, la mathématicien américien Moore décide d'accoler 4 courbe de Hilbert entre-elles afin d'obtenir un tracé fini de la courbe de Hilbert.
ATTENTION : la courbe de Moore est approchée à l'odre n, alors que les 4 courbes de Hilbert reliées entre elles sont approchées à l'ordre n-1.
Voici un exemple où la courbe de Moore est approchée à l'ordre 4 tandis que les 4 courbes de Hilbert sont approchée à l'ordre 3 :
Voici ce qui se passe lors des premières itérations :

La courbe de Lebesgue en Z (1904)
En 1904, la courbe de Koch est inventée
En 1904, le mathématicien suédois Helge von Koch créé la courbe de Koch à partir d'un segment de droite, en modifiant récursivement chaque segment de droite de la façon suivante:
1. Il divise le segment de droite en trois segments de longueurs égales.
2. Il construit un triangle équilatéral ayant pour base le segment médian de la première étape.
3. Enfin, il supprime le segment de droite qui était la base du triangle de la deuxième étape.
Ces instructions nous donne la courbe de Koch suivante:
La construction extrêmement simple de Koch a à nouveau abouti à une courbe continue qui n’admet pas de tangente.
Mais cette, la courbe de Koch fois est plus simple à réaliser que celle de la fonction de Weierstrass.
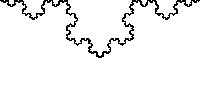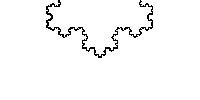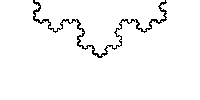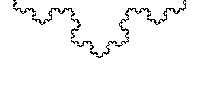
En 1915, le tamis de Sierpiński fait son apparition
Cette construction consiste à prendre un triangle quelconque et à lui retirer le triangle formé par les points milieux de ses trois côtés. Pour chacun des trois triangles ainsi formés, on retire le triangle central de la même façon et on poursuit le procédé jusqu’à l’infini.
Après que ce processus soit répété une infinité de fois, on obtient le triangle de Sierpiński.
Remarque :
Ce même processus peut être généralisé à tous les polygones convexes réguliers.
La carpette de Sierpiński / Le tapis de Sierpiński (1916)
Le principe de construction est de prendre un carré et de lui retirer toujours le carré central.
Après que ce processus soit répété une infinité de fois, on obtient la carpette de Sierpiński.
Il existe également des variantes au carré de Sierpiński :
http://www.mathcurve.com/fractals/sierpinski/carresierpinski.shtml
Le pentagone de Sierpiński, une variante du Pentaflake de Dürer !
Cette construction est analogue à la construction du triangle de Sierpinski : on met à l'échelle un triangle et on le traduit en trois exemplaires.
Dans ce cas, nous voulons mettre à l'échelle un pentagone et les traduire en cinq exemplaires. Les cinq petits pentagones (en rouge) sont placés de sorte qu'ils soient à l'intérieur du plus grand pentagone (décrite dans le noir), comme illustré dans la figure suivante :

En appliquant cette idée à un pentagone mais en y ajoutant un pentagone inversé au centre pour chaque itération, on retrouve le pentagone de Dürer (présenté plus haut).
Il existe également l'hexagone de Sierpiński, ainsi que l'octogone de Sierpiński (surnommé également "napperon de Koch") qui sont construits sur le même modèle que le pentagone de Sierpiński.
Par la suite, les figures de Sierpiński construites en 3D
Tétraèdre de Sierpinski
Le tétraèdre de Sierpiński est la version en trois dimensions du triangle de Sierpinski.
Comme il fait partie d'un tétraèdre régulier et est divisé en deux pour éliminer les tétraèdres secondaires qui ne sont pas aux extrémités.
Il faut réitérer la procédure dans chaque tétraèdre formé.
Après que ce processus soit répété une infinité de fois, on obtient le tétraèdre de Sierpiński :
L'éponge de Menger (1926)
L'éponge de Menger, parfois appelée éponge de Menger-Sierpinski, est un solide fractal.
Il s'agit de l'extension dans une troisième dimension de l'ensemble de Cantor et du tapis de Sierpinski.
Après que ce processus soit répété une infinité de fois, on obtient alors l'éponge de Menger.
Le plus intéressant avec cette éponge, c'est que lorsqu'on la coupe transversalement.
Regarder bien la forme de la section :
INCROYABLE !
A voir également
http://www.mathcurve.com/fractals/gosper/gosper.shtml
http://ecademy.agnesscott.edu/~lriddle/ifs/ksnow/ksnow.htm
http://ecademy.agnesscott.edu/~lriddle/ifs/heighway/twindragon.htm
D'autres fractales

Comment mesurer la longueur des frontières des pays ?
Qu'est-ce-que le mouvement Brownien ?
Vous y trouverez les réponses en cliquant ICI.

Dans les années 1970, le mathématicien Benoît Mandelbrot (1924,2010) eut l'idée de regrouper trois courbes de von Koch pour former une figure ressemblant à une sorte de flocon de neige, que l'on appelle le Flocon de Koch :
Le flocon de Koch peut également se reproduire de cette façon :
Ingenious, isn't it ?
Benoît Mandelbrot est le premier mathématicien a avoir inventé le mot "Fractale".
La biographie de Mandelbrot est donnée ICI.
Mandelbrot a réussi a assemblé tout ces morceaux d'un immense puzzle.
La dimension fractale est née !
Mandelbrot fit égalementfait le lien entre les Fractales de la Nature et les Mathématiques.
Je vous propose de regarder où se trouvent ces fameuses Fractales dans notre quotidient.
Vous DEVEZ ABSOLUMENT voir cette partie !
Començons la visite en cliquant ICI.
 A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?