Les fractales dans la Technologie
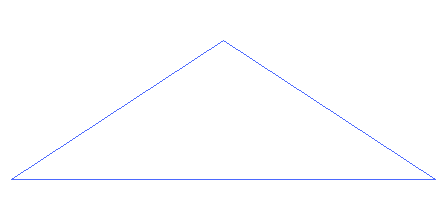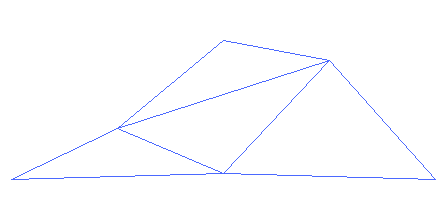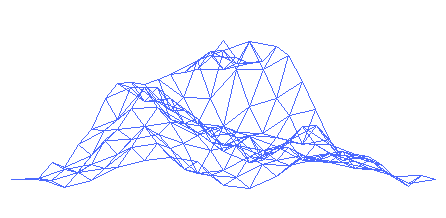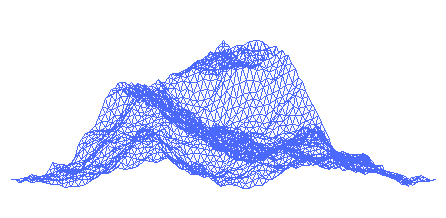
Les fractales en informatique (films, montagnes, 3D...)
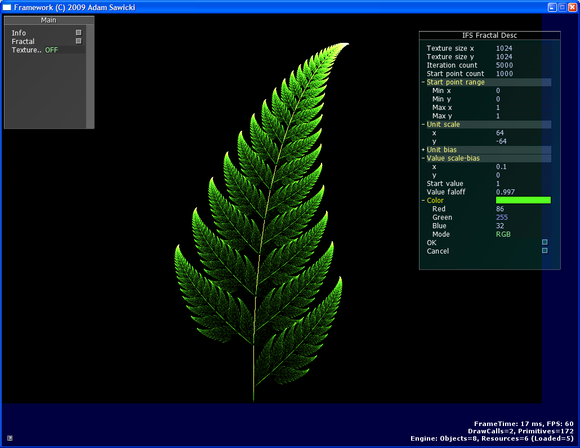
Les fractales IFS
http://fractalesland.free.fr/Nouveau%20dossier/autre%20cadre%20(applications%20fractales).htm
L'une de ces nombreuses applications a lieu dans l'informatique, et plus précisément dans le domaine de la compression d'images. En effet, il est possible de coder une image en utilisant la théorie des fractales et notamment celles des fractales IFS (Systèmes de Fonctions Itérées). Ces fractales sont obtenues par des formules mathématiques itératives, c'est-à-dire répétitives. Les IFS permettent de décrire les paysages naturels, les nuages, les plantes et les arbres avec une grande fidélité et un grand réalisme.
On repère dans l'image les parties qui présentent une certaine similarité (on parle d'autosimilarité ; notion vue auparavant), c'est-à-dire des parties qui peuvent s'exprimer les unes par rapport aux autres (avec une possibilité de transformation). Les applications qui nous permettent de modéliser ces autosimilarités et autres transformations de l'image sont les informations qui seront utilisées pour sauvegarder l'image.
Ainsi le "poids" de l'image sera considérablement réduit.
La compression fractale est très utilisée dans les jeux vidéos et dans le cinéma pour la création de paysages en images de synthèse comme les montagnes, les rivières, les arbres, les nuages
...
Voici quelques animations supplémentaires :
http://fpassebon.pagesperso-orange.fr/fractales.html#
Pour aller plus loin :
http://www.hiddendimension.com/FractalMath/IFS_Fractals_Main.html
http://en.wikipedia.org/wiki/Barnsley's_fern#Example:_a_fractal_.22fern.22
Les fractales issues du L-Système
Un L-Système ou système de Lindenmayer est une grammaire formelle, inventée en 1968 par le biologiste hongrois Aristid Lindenmayer, qui consiste à modéliser le processus de développement et de prolifération de plantes ou de bactéries.
Au départ, Lindenmayer conçoit sa formalisation comme un modèle de langages formels qui permet de décrire le développement d'organismes multicellulaires simples. À cette époque il travaille sur les levures, les champignons et des algues. Mais sous l'influence des théoriciens et des praticiens de l'informatique, ce système a conduit à des familles de langages formels et aussi à des méthodes pour générer graphiquement des plantes idéalisées très complexes.
Le concept central des L-système est la notion de réécriture. La réécriture est une technique pour construire des objets complexes en remplaçant des parties d'un objet initial simple en utilisant des règles de réécriture.
Pour aller plus loin :
http://www.hiddendimension.com/FractalMath/LSystem_Fractals_Main.html
Les effets spéciaux dans le film Star Wars
Vidéo à regarder entre les minutes 12:00 et 13:40
Choisir son propre logiciel de modélistation
Les fractales en électricité et en électronique
Les figures de Lichtenberg
http://www.laboiteverte.fr/des-fractales-avec-un-accelerateur-de-particules/
Todd Johnson fait passer du plexiglas dans un accélérateur de particules qui le bombarde de protons qui se retrouvent piégés dedans, accumulant ainsi plusieurs millions de volts
d’électricité.
Il suffit alors de frapper le plexiglas avec un marteau et le choc libère l’électricité qui s’échappe en le faisant fondre en suivant des figures de
Lichtenberg.
On retrouve les mêmes formes sur la peau des gens frappés par la foudre.
Il peut ensuite délimiter des formes en utilisant des crayons à la mine de plomb qui stoppent la propagation de l’électricité en la conduisant.

Voici une vidéo qui montre le phénomène :
Pour aller plus loin avec les figures de Lichtenberg
http://www.capturedlightning.com/frames/lichtenbergs.html
http://www.capturedlightning.com/frames/interesting.html
Un CD exposé aux radiations
Voici les images montrant les motifs provoqués par les décharges électriques lorsque l'on place un CD dans un micro-ondes durant une durée environ 4 secondes :
Le papillon de Hofstadter

Le papillon de Hofstadter est un être mathématique utilisé en physique afin de décrire le comportement théorique d'électrons dans un champ magnétique.
![The Hofstadter butterfly for an hexagonal lattice subjected to a magnetic flux Φ. Here one sets α=β=0. (bottom) The same butterfly spectrum in the vicinity of the Dirac regime E∈[−1,1].](https://image.jimcdn.com/app/cms/image/transf/dimension=580x10000:format=png/path/s51fc61a5707b6420/image/i9a2c400b74d349d4/version/1422812402/image.png)
Les fractales dans l'isolation sonore
http://fractalesland.free.fr/Nouveau%20dossier/autre%20cadre%20(applications%20fractales).htm
Ce qui a été découvert sur les côtes maritimes (comme sur la côte de Bretagne) a trouvé une application dans... l'insonorisation !
L'effet d'amortissement du relief des plages du à leurs contours fractals peut se faire au niveau des ondes sonores (qui ne sont que des vagues d'air!). Il suffit de répéter sur une surface un motif fractal simple (en relief bien sûr), qui augmentera ainsi la surface de contact avec l'onde. Comme cette surface est brisée l'onde sera très peu réfléchie par le mur. A une fréquence de 250 Hz, ce mur ne renvoie que 15% de l'intensité sonore, alors qu'un mur classique renvoie 45% de cette même intensité. Mais malgré la simplicité du motif, le moulage de telles formes n'est pas facile. Bien que le prix soit plus élevé que pour un mur classique, ces murs fractals devraient border bientôt les routes des grands axes de circulation...
http://geoffreyhistoire.pagesperso-orange.fr/fractales/bruit.html
Les ondes émises, en percutant une surface fractale sont théoriquement soumises à une infinité de résistance de la part de celle-ci. Ainsi, une côte totalement fractale amortirait la totalité des
vagues d'un seul coup.
Cette idée peut alors être reprise pour amortir un grand nombre d'ondes que l'on ne souhaiterait pas voir se propager. C'est le cas des ondes sonores sur nos routes.
L'utilisation d'un mur de géométrie fractale pour lutter contre le bruit apporte des avantages pour deux raisons :
- il peut placer une surface réelle plus importante que la surface apparente, ce qui permet d'exploiter au mieux une idée courante en acoustique qui est que l'absorption sonore est
proportionnelle à la surface développée au contact des ondes sonores.
-les anfractuosités nombreuses permettent un phénomène de localisation des ondes qui se retrouvent bloquées.
Les tests en laboratoire ont montré que la réflexion des ondes sonores était diminuée de 8 dB, tandis que la transmission - les sons capables de traverser l'écran - était réduite de 57 dB. Ceci représente une absorbtion 4 fois plus importante que les autres murs antibruit.

Les fractales pour gagner de la place
Les antennes fractales
Dans notre société où tout le monde possède un téléphone portable, où, avec toutes sortes d'appareils, toutes sortes d'informations se reçoivent (depuis des satellites ou des antennes
hetziennes...), les exigences de miniaturisation deviennent de plus en plus importantes.
Mais comment miniaturiser une antenne tout en gardant autant de longueur de réception, et donc d'efficacité de réception, que lorsque l'antenne est totalement dépliée ?
La réponse est dans les arbres!
Il "suffit" de fracturer l'antenne autant de fois que possible de façon fractale, c'est-à-dire en diminuant la longueur à chaque fractionnement.

Cette miniaturisation fut une première réussite pour les chercheurs qui travaillaient sur les antennes fractales. En effet, outre l'ergonomie et le gain considérable de place, on pouvait perfectionner les performances de l'antenne (tout simplement en ajoutant des branches et des ramifications).
L'autosimilarité de la fractale permet la captation de différentes fréquences.

Découvert au XXème siècle, ce système d’antenne va marquer une grande avancée dans la télécommunication.
La compression fractale
L'objectif de la compression est de réduire le nombre d'octets tout en gardant l'image intacte.
Sur l'image ci-dessous, si on prend tous les carrés rouges on remarque qu'ils contiennent le meme schéma : un quart de cercle orienté dans le meme sens à chaque fois. Ainsi, au lieu d'enregistrer
pixel par pixel comme le font les autres formats (BMP ou JPEG) en utilisant 3 octets par pixel (1 octet pour determiner le niveau de rouge + 1 pour le niveau de vert + 1 pour un niveau de bleu),
il suffit de n'enregistrer que le contenu d'un seul carré rouge, ce qui fait ici environ un kiloctect (soit 1024 octects).
A ces 1024 octets, il faut ajouter 2 à 5 octets pour indiquer l'emplacement des carrés similaires.
Explication : Pour indiquer l'emplacement du carré, on a besoin de 2 nombres : l'abscisse et l'ordonnée du centre du carré. mais il n'existe que 256 versions d'un octect car un octect est un
enchainement de 8 nombres, 0 ou 1. Donc le nombre d'octets différents possibles équivaut à 28=256. Ainsi, si l'image est plus grande que 256 pixels, on a besoin de deux octets voir plus.
Une fois que l'ordinateur sait ou doit se placer le carré (ou tout autre forme géometrique), il a besoin de le redimensionner. En effet, certains carrés ne sont pas tous à la meme taille, comme
ci-dessous :

On constate qu'il y a un blanc car la réplique est mal adaptée. Pour le combler, il faut étirer l'image. Pour celà, on a encore besoin de 2 nombres: la distance entre le centre du carré et un des
côtés horizontal et celle entre le centre et un des côtés vertical, ce qui ne prend le plus souvent qu'un seul octet.
Maintenant que l'on a entré les bonnes distances, un autre problème se pose : en effet, les schemas qui présentent une similarité n'ont pas tous la même couleur, comme ci-dessous :

Pour remédier à ce problème, les logiciels de decompression fractale utilisent une technique qui consiste à foncer ou à claircir le schéma copié en fonction de la luminosité qui entoure le
carré.
Sur l'exemple ci-dessus, le coquillage est plus foncé, donc le programme va chercher comment le foncer de maniere adéquate. Il va comparer les couleurs de deux points qui se touchent mais dont
l'un est dans le carré copié et l'autre à l'exterieur.
Par exemple, le point a l'éxterieur a pour indices de couleur 138 111 094 et le point à l'interieur 233 232 186, donc pour l'ordinateur il va falloir ramener tous les points à l'intérieur du
schema au niveau de ceux à l'extérieur :
-pour le rouge de 233-138=95
-pour le vert de 232-11=121
-et pour le bleu de 186-94=92.
A ce moment, on retrouve le coquillage comme il était avant la compression.
Un dernier problème se pose pour le carré vert (ci-dessus). En effet, celui ci n'est pas dans le bon sens. Pour y remédier, il suffit de faire faire au carré rouge une symétrie où l'axe de
symetrie est une droite verticale (dans ce cas ci), on peut aussi y ajouter une rotation dans le cas où la symétrie centrale ne suffirait pas.
Voici une animation pour comprendre la compression fractale :
http://www.eurecom.fr/~image/DEMOS/FRACTAL/francais/index.html
Le Test de Blaine
http://fr.wikipedia.org/wiki/Fractale#Utilisations_industrielles
Surface spécifique de Blaine : la finesse de broyage d'un ciment est exprimée en termes de surface spécifique (cm²/g) et mesurée par la méthode de
Blaine, dite de perméabilité à l'air, utilisant la loi de Darcy, et la loi de Kozeny-Carman qui établit que la traversée d'un lit de granules par un fluide est affectée
par la surface spécifique des granules.
Ainsi, en calculant la durée que met un gaz sous pression à traverser un volume donné de granules, on en déduit la surface des granules. Plus le broyage est fin, plus la surface calculée est importante.
Cette expérience se produisant dans un volume déterminé, on peut imaginer obtenir une surface développée infinie en broyant toujours plus finement le ciment. Il s'agit là d'une utilisation industrielle d'un modèle expliqué par les mathématiques fractales (un objet de dimension de mesure finie, borné par une frontière de dimension, de mesure tendant vers l'infini).

Voici désormais les deux domaines qui vous restent à explorer :
Il vous reste également le thème sur la nature fractale de l'Univers si vous ne l'avez pas encore fait :
 A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?