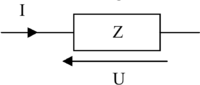
Les impédances complexes
En électricité, on peut caractériser le comportement d'un dipôle passif linéaire en régime sinosoïdal avec un nombre complexe que l'on appelle l'impédance complexe.
La notion d'impédance
La loi d'Ohm généralisée aux circuits en courant alternatif
L'impédance électrique mesure l'opposition d'un circuit électrique au passage d'un courant alternatif sinusoïdal.
La définition d'impédance est une généralisation de la loi d'Ohm dans l'étude des circuits en courant alternatif.
En effet, dans un signal alternatif sinusoïdal, on constate que d'autres éléments, qui ne sont pas des résistances, répondent aussi à cette loi. Puisque ce ne sont pas des résistances, on ne peut pas utiliser la lettre R, ni les appeler « résistances ».
Etymologie : "to impede" en anglais = « retenir », « faire obstacle à ».
On donne alors l'égalité complexe suivante :
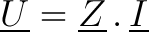
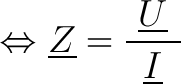
Module et argument de l'impédance
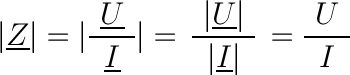
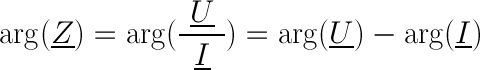
Impédance, résistance et réactance
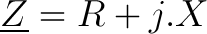
R est la partie réelle dite résistive et X est la partie imaginaire dite réactive ou réactance.
L'impédance peut également se noter sous forme exponentielle; en effet :
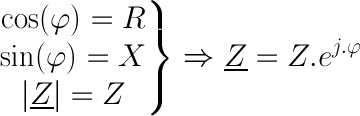
Une impédance dont la partie imaginaire est positive sera qualifiée d'impédance inductive.
Si la partie imaginaire est négative, on parle alors d'impédance capacitive.
La notion de conductance complexe
La conduction est par définition l'inverse de la résistance pour un courant continu.
La conductance est ainsi l'inverse de l'impédance pour un courant alternatif.
On note alors :

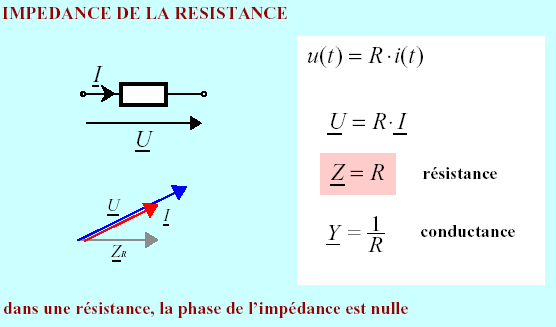
Impédance de la résistance
Les définitions de la résistance et de l'impédance permettent d'écrire :

R correspond à la résistance en ohm.
Ainsi, on a que :

Cette impédance est purement réelle, son module vaut R et son argument est nul.
Impédance de l'inductance
Impédance de la capacité
Le cours sur l'électricité s'arrête ici (mais il reste plein de chose à apprendre en électricité (RLC complexe ...).
Découvrez désormais les Fractales en cliquant ICI.
 A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?