Méthode de résolution des trinômes dans R

Une fonction du second degré est définie par :

"a" s'appelle le coefficiant du carré, "b" est le coefficiant de la variable et "c" est une constante.

"a" joue un rôle sur l'orientation et la forme de la courbe tandis que "c" ne sert qu'à déplacer la courbe vers la direction voulue.

Une fonction du second degré s'appele aussi trinôme car elle est contituée par 3 monômes (de degré 2, 1 et 0). 

Elle peut donc aussi s'écrire de cette manière :

Cette forme d'écriture de f s'appelle la forme développée de f.

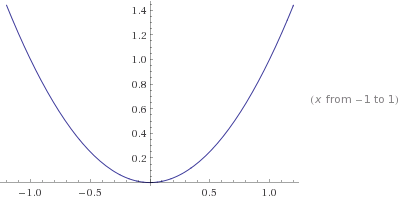
La courbe des fonctions trinômes s'appelle une parabole.

Il existe une forme appelée canonique de f qui permet de ne faire apparaître qu'une seule fois la variable x dans l'équation de f(x).

Pour obtenir cette forme de f, il y a 3 étapes à effectuer.

On commence par factoriser le trinôme tout entier par "a"; on a alors :

Dans la parenthèse contenant les deux variables "x", nous voulons ne plus qu'obtenir qu'une seule variable x.

Nous avez sûrement dû voir cette identité remarquable vue au collège :

REMARQUE : 

Normalement, elle se note (a+b)^2 = a^2+2.a.b+b^2 , mais les "a" et "b" s'y trouvant pourraient porter à confusion avec le coefficiant du carré "a" et le coefficiant de la variable "b", alors qu'ils n'ont rien avoir ici (d'où l'emploi des lettres "e" et "f" ).

Dans notre trinôme, nous voulons obtenir l'expression de gauche de l'égalité à partir de celle de droite. Notre objectif est de se forcer à obtenir l'expression de droite avec ce que l'on a dans notre parenthèse.

On a donc :

Cependant on préfèrera l'écrire sous cette écriture :

Vous avez compris, on pose que :

Delta, c'est ce qu'on appelle un discriminant.

On ne pose pas delta pour un simple plaisir, vous vous en doutez bien.

Grâce au signe Delta, on peut savoir si notre trinôme peut se factoriser ou non.

Voyons celà d'un peu plus près.

On distingue 3 cas remarquables du discriminant Delta :

Lorsque delta est strictement positif, on peut noter f(x) de cette manière :

Il faut que delta soit strictement positif car une racine carré n'est définie sur R que pour les quantités positives (donc aussi nulles).

D'après une autre identité remarquable du collège :

Par similitude avec f(x), on a du coup :

Cependant, on écrit f(x) sous la forme suivante :

Cette fois puisque delta est nul, alors on peut noter f(x) de cette manière :

f(x) se trouve directement sous sa forme factorisée !

Quand Delta est négatif, le trinôme f(x) n'est pas factorisable (valable uniquement dans R ! ).

La parabole coupe l'axe des abscisses lorsque qu'elle admet en une ordonnée nulle (y = 0), donc lorsque :  f(x) = 0.

Or comme nous savons que f(x) est factorisable pour un delta strictement positif ou nul (donc pour un delta positif), alors l'équation f(x) = 0 est résolvable par produits de facteurs nuls !

On rappelle que f(x) s'écrit sous cette forme factorisée avec un delta strictement positif :

Passons maintenant au calcul de f(x) = 0 :

En effet, il n'est pas possible que a = 0 car si a = 0, on n'obtient pas un polynôme du second degré f(x) = a.x^2+b.x+c mais une fonction affine f(x) = b.x+c . Or on réalise cette égalité pour un trinôme.

Finalement, quand Delta est strictement positif, la parabole rencontre l'axe des abscisses en 2 abscisses notées x_1 et x_2 tels que :

x_1 et x_2 sont appelées les racines de f .

On rappelle que f(x) s'écrit sous cette forme factorisée avec un delta de valeur nulle  :

Passons maintenant au calcul de f(x) = 0 :

Finalement, quand Delta est nul, la parabole rencontre l'axe des abscisses un unique point x_0  appelé racine double (car x_1 et x_2 confondus en un unique point x_0) tel que :

  Avec un delta strictement négatif, f(x) ne coupe jamais l'axe des abscisses.

Il est donc normal de ne pas avoir de valeur pour laquelle la parabole coupe l'axe des abscisses.

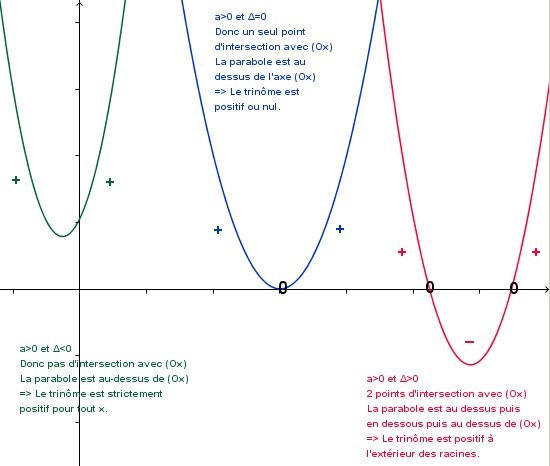
Je vous propose de comparer les représentations de chacune des situations pour bien se visualiser les différentes situations.

Je vous ai fait un tableau qui affiche les 6 cas différents que peut rencontrer un trinôme.

Ainsi, si a > 0 :

Si a < 0 :

Remarque :

Le sommet de la parabole se situe toujours à une abscisse de -b/(2.a) et a donc pour maximun (lorsque le coefficiant du carré a>0) ou pour minimum (lorsque le coefficiant du carré a<0) la valeur :

Si vous voulez vous entraîner à factoriser un trinôme, regarder cette vidéo :

La même vidéo montre les variations d'une fonction trinôme selon les cas :

Voici également un lien qui renvoie à un pdf avec un cours sur le second degré détaillé.

http://www.ac-grenoble.fr/lycee/vincent.indy/IMG/pdf/second-degre.pdf 

Voici un lien qui permet de faire ses propres résolutions de Delta avec des aides :

http://math.eepc.fr/equa2.htm 

Maintenant que vous savez comment résoudre ces équations dans R, passons à l'ensemble C !

Pour cela, cliquez ICI.