A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
Les propriétés sur les nombres complexes conjugués
Cette rubrique est un peu plus "scolaire" car je ne vois comment la faire autrement...
A la découverte de la notion de conjugué :
Soit z = a + b.i un nombre réel.
On dit que z barre est le conjugué de z si :
z et z barre :
Pour un même nombre complexe z = a+b.i, il existe des propriétés tout à fait intéressantes dessus.
Somme entre z et z barre :
Démonstration :
Différence entre z et z barre :
Démonstration :
Produit entre z et z barre :
Démonstration :
z barre barre
Le z barre barre n'est pas si barbare que ça ;-)
En effet :
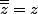
L'inverse de z
Démonstration :
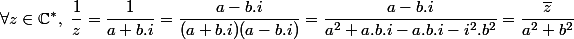
L'inverse de z barre
Démonstration :
z_1 barre et z_2 barre :
Pour toute la suite de ce chapitre on posera z_1 et z_2 deux nombres complexes différents tel que :
Le conjugué de la somme est la somme des conjugués
Démontration :
Le conjugué de la différence est la différence des conjugués
Démonstration :
Le conjugué du produit est le produit des conjugués
Démonstration :
Elle se fait en 2 parties.
D'abord on calcule le conjugué du produit, puis le produit des conjugués et on compare les résultats obtenus pour chacun.
1. Calcul du conjugué du produit :
2. Calcul du produit des conjugués :
L'égalité énoncé plus haut est donc bien respectée.
Le conjugué de l'inverse est l'inverse du conjugué
Démonstration :
Elle se fait de la même manière que précédemment.
1. Calcul du conjugué de l'inverse :
2. Calcul de l'inverse du conjugué :
L'égalité énoncé plus haut est donc à nouveau donc bien respectée.
Le conjugué du quotient est le quotient des conjugués
Pour démontrer celà, il nous faudra utiliser les propriétés démontrées précédemment.
Démonstration :
En résumé :
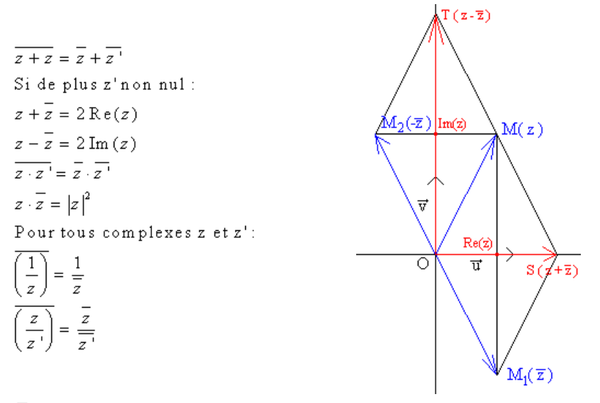
Si vous voulez, il existe une super vidéo qui récapitule tout cela :
Passons maintenant à la méthode de résolution des équations du second degré dans C, c'est à dire ayant un Delta strictement négatif.
Pour cela, cliquez ICI.
