A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
Exposant de Lyapunov
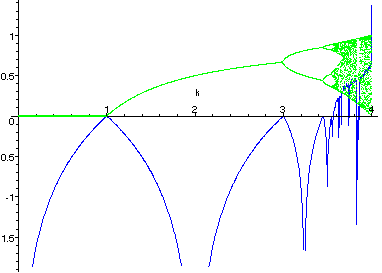
Certains systèmes dynamiques (systèmes qui décrivent dans l'espace un état qui évolue dans le temps) sont très sensibles aux petites variations de leur condition initiale. Ces variations peuvent rapidement prendre d'énormes proportions. Le mathématicien russe Alexander Lyapunov s'est penché sur ce phénomène et a développé une quantité permettant de mesurer la vitesse à laquelle ces petites variations peuvent s'amplifier. Cette quantité appelée « exposant de Lyapunov » mesure en fait le degré de sensibilité d'un système dynamique.
En fait l'exposant de Lyapunov est synonyme d'instabilité et de chaos.
Cette quantité sert à mesurer le degré de sensibilité d'un système comme celui du haut, suite à une variation infinitésimale de sa condition initiale Po. Un système sensible à de très petites variations de la condition initiale Po (une des caractéristiques des systèmes chaotiques), donc que le système est classique et obéit aux lois de la dynamique (réversibilité, etc.), alors il aura une quantité λ positive.
A l'inverse, la quantité λ sera négative si de petites variations de Po n'ont aucun effet à long terme sur le système.
Visualisation - Fractale de Lyapunov
