Les nombres de Feigenbaum

Etonnament l'itération de nombreuses fonctions simples répétées de nombreuses fois en prenant pour valeur le résultat de l'itération x(t+1)=f[x(t)] aboutit à des courbes de bifurcations similaires avec des constantes de bifurcation IDENTIQUES, appelées constantes de Feigenbaum.

Ces transitions apparaissent aussi dans de nombreux processus physiques, notament ceux décrit par des équations différentielles non linéaires.

http://villemin.gerard.free.fr/Wwwgvmm/Chaos/Chaos.htm

http://fr.wikipedia.org/wiki/Nombres_de_Feigenbaum

http://mathworld.wolfram.com/FeigenbaumConstant.html

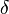La première constante de Feigenbaum  est définie comme la limite du rapport entre deux intervalles successifs de la bifurcation :

La première constante de Feigenbaum 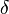 peut être utilisée pour prédire quand le chaos arrivera dans un tel système.

La deuxième constante de Feigenbaum est définie comme la limite du rapport entre deux distances successives entre les branches les plus proches de x_m (= maximum de la fonction f)

Ces deux constantes s'appliquent à une large classe de systèmes dynamiques (ceux pour lesquels f présente un extremum quadratique). 

On conjecture que ces deux nombres sont transcendants (et indépendants des autres constantes usuelles telles que  ou ) mais cela n'a pas encore été prouvé.