Le théorème de Boucherot
Prérequis
Qu'est-ce-qu'une puissance active et réactive ?
La puissance active
Démonstration
Nous savons que la puissance est le produit de la tension avec l'intensité pour chaque seconde.
Dans un courant alternatif, nous avons affaire à une courbe sinusoïdale.
On parle alors de puissance active pour les courants alternatifs.
Dans un premier temps, nous allons chercher l'expression de la fonction de la puissance instantanée au cours du temps p(t).
On sait d'après les propriétés de trigonométrie que :


Et que :

Si on fait la somme membre à menbre, on obtient :

On a ainsi que :

De plus, sachant les trois relations suivantes, on peut en déduire l'expression de la puissance instantanée en fonction du temps p(t) :


D'après la formule de trigonométrie donnée ci-dessus, on peut arranger l'écriture de p(t); en effet :


Si on remet tout en ordre, on a que :

Or nous cherchons ce que vaut la puissance active, c'est à dire la puissance MOYENNE.
Quand on analse notre expression de la puissance active au cours du temps, on remarque deux choses :
- U.I cos φ est indépendant du temps t
- U.I cos (2ωt-φ) est une fonction sinusoïdale dont la variable est le temps donc sa valeur moyenne est nulle (ce qui semble logique).
Finalement, notre fonction associée à la puissance instatanée au cours du temps est donnée par :

Maintenant que nous connaissons l'expression de cette fameuse puissance instantanée au cours du temps, nous pouvons déterminez celle de la puissance active.
Pour calculer la valeur de cette puissance active au cours du temps, il est utile d'utiliser la formule de valeur moyenne d'une fonction f(x) à l'aide du calcul intégrale, qui énonce :


L'expression de la puissance active P_a à chaque instant d'une période T est donnée par :
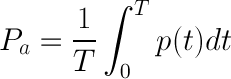
Le théorème de Boucherot
Enonciation générale
Les puissances active et réactive absorbées par un groupement de dipôles sont respectivement égales à la somme des puissances actives et réactives absorbées par chaque élément du groupement.
Puissance active
Si un circuit contient n composants absorbant chacun une puissance active P_i, alors les puissances actives du circuit vérifient :

Puissance réactive
De même, si un circuit contient n composants absorbant chacun une puissance réactive Q_i, alors les puissances réactives du circuit vérifient :

 A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?


