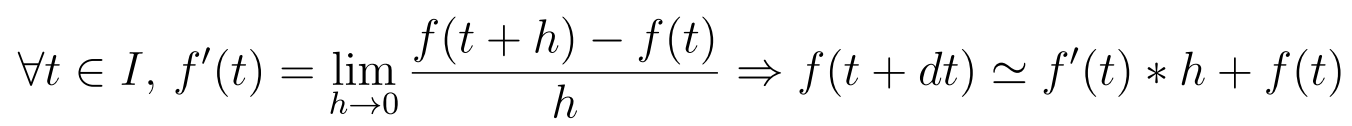La réaction oscillante de Belousov-Zhabotinsky (BZ)
Dans cet article, je fais vous parler d'une notion qui est à l'intersection entre deux disciplines : la chimie et l'informatique.
Je vais vous parler plus précisément de réactions chimiques dites "oscillantes". Lorsque de telles réactions se produisent, on voit clairement des motifs ou des couleurs qui varient au cours du temps comme s'ils oscillaient.
En première approche, ce type de réaction paraît dure à expliquer. Cependant deux scientifiques Belousov et Zhabotinsky ont contribué à la découverte et à l'explication de cette réaction. Vous verrez qu'en fait cette réaction recèle bien des surprises par la suite.
A) Qui sont Belousov et Zhabotinsky ?
Ces deux personnes sont en fait des scientifiques russes. Sur l'image à droite, nous pouvez voir le chimiste Boris Pavlovich Belousov qui a découvert la réaction et sur l'image à gauche le physicien Anatol Zhabotinshy qui a expliqué mathématiquement la réaction chimique à l'aide de la cinétique chimique. Ces deux personnes ont toutes les deux contribuées d'une manière ou d'une autre à l'étude de cette réaction oscillante qui porte désormais leurs noms : la réaction de Belousov-Zhabotinsky (en abrégé réaction BZ ou réaction B-Z).

B) Visualisation de la réaction B-Z au cours du temps :
Réaction B-Z vue de profil
On voit bien sur cette expérience que la solution change de couleur par cycles.
Une autre réaction de BZ vue depuis le dessus d'un bécher
On y voit des motifs qui font penser à ceux de la morphogénèse conçue par le célèbre mathématicien Alan Turing que l'on observe dans tous les systèmes biologiques !
C'est justement la cinétique chimique qui permet d'expliquer de telles similitudes entre cette réaction et la morphogénèse de Turing.
C) Explication du phénomène d'oscillation à l'aide de la cinétique chimique :
Afin de connaître la vitesse d'une réaction chimique "i", la cinétique chimique fait appel à des constantes de vitesse notées souvent k_i.
Par exemple, pour une réaction dite du premier ordre, la vitesse de disparition v d'un réaction A s'écrit :
![]()
Rmq : On peut dans ce cas particulier d'une réaction du premier ordre définir la constante de vitesse k comme l'opposé du rapport entre la variation de la concentration en réactif A au court du temps par rapport à la concentration en réactif A.
Les constantes de vitesse k_i peuvent être déterminées expérimentalement en suivant au cours du temps la concentration des espèces chimiques qui interviennent dans la réaction. En fait, on utilise différentes concentrations initiales des espèces chimiques afin de pouvoir en tirer les k_i de toutes les réactions.
Si on fait un bilan sur les vitesses d'apparition et de disparition des espèces non spectatrices dans la solution, on peut alors lier les constantes de réaction k_i avec les concentrations des différentes espèces.
On peut ainsi aboutir à un système d'équations différentielles qui sont couplées entre-elles.
Il faut alors résoudre un système d'équations différentielles couplées pour en tirer toutes les constantes de réaction k_i puisque l'on a suivi au cours du temps d'évolution des concentrations en espèces chimiques lors de la réaction "i".
Connaissant l'évolution des concentrations des différentes espèces dans notre milieu réactionnel, on peut alors savoir quels sont les ions qui ne se sont pas liés entre-eux.
Les ions qui ne se sont pas liés avec d'autres ions dans la solution peuvent "exprimer librement leurs couleurs" : la solution se colore alors.
Cependant comme chaque ion est neutralisé par un autre ion au fur et à mesure que la réaction progresse dans le temps, alors la solution change de couleur au cours du temps.
En résolvant le système d'ED couplées, on va pouvoir alors savoir les concentrations des différentes espèces au cours du temps, et donc la couleur de la réaction au cours du temps ! C'est ce que nous allons faire dans la partie D.
ATTENTION : Dans la partie D, on suppose que les constantes de réaction k_i et les ordres de réaction sont connus, ainsi que les concentrations initiales des espèces que l'on introduit dans le bécher (sans tenir compte ici des espèces qui n'interviennent pas dans la réaction proprement dite) contrairement à avant où on connaissait les concentrations et leurs variations pour en déduire des constantes de réactions k_i et les ordres de réaction.
Allons-y.
D) Approximation du système d'équations différentielles (ED) couplées :
D.1) Présentation du système d'ED couplées représentatif de la réaction de BZ
Le système d'ED couplées qui est écrit ci-dessous est celui correspondant à une réaction de B-Z. Le voici justement :

où :
-> A=1 //concentration initiale en bromate BrO3- (invariante lors de la réaction)
->f=1 //f est traité comme un paramètre ajustable compris entre 0,5 et 2,4
->k1=0.05, k2=0.8, k5=1.58, k6=0.2, k7=0.4 sont des constantes de vitesse de réactions (par hypothèses, les k_i sont connus).
Les lettres x(t),y(t) et z(t) correspondent respectivement à la concentration en ions bromure Br-, en acide bromeux HBrO2 et en cerium-IV Ce4- au cours du temps.
Je ne vais pas détailler comment obtenir ce système d'ED couplées, cependant ces équations sont issues de la cinétique chimique pour une réaction de BZ donnée.
D.2) Approximation de ce système d'ED couplées pour la résolution numérique :
L'approximation de chaque équation différentille se fait à l'aide de la méthode d'Euler visant simplement à approximer une dérivée par son taux d'accroissement; pour un intervalle de temps "I" et un pas "h" suffisamment petit, on a :
Je vous conseille de lire un article du site zestedesavoir.com pour en savoir plus à ce sujet (cliquez ICI pour cela).
Comme ici on a trois équations différentielles, il faudra alors appliquer trois fois la méthode d'Euler pour résoudre de système.
Si on approxime le système d'ED couplées précédant pour un pas h=10^-3, on a alors :

On peut de cette manière connaitre petit à petit les concentrations x,y et z des différentes espèces chimiques de la solution. On étudiera cette réaction sur l'intervalle de temps I=[0;100].
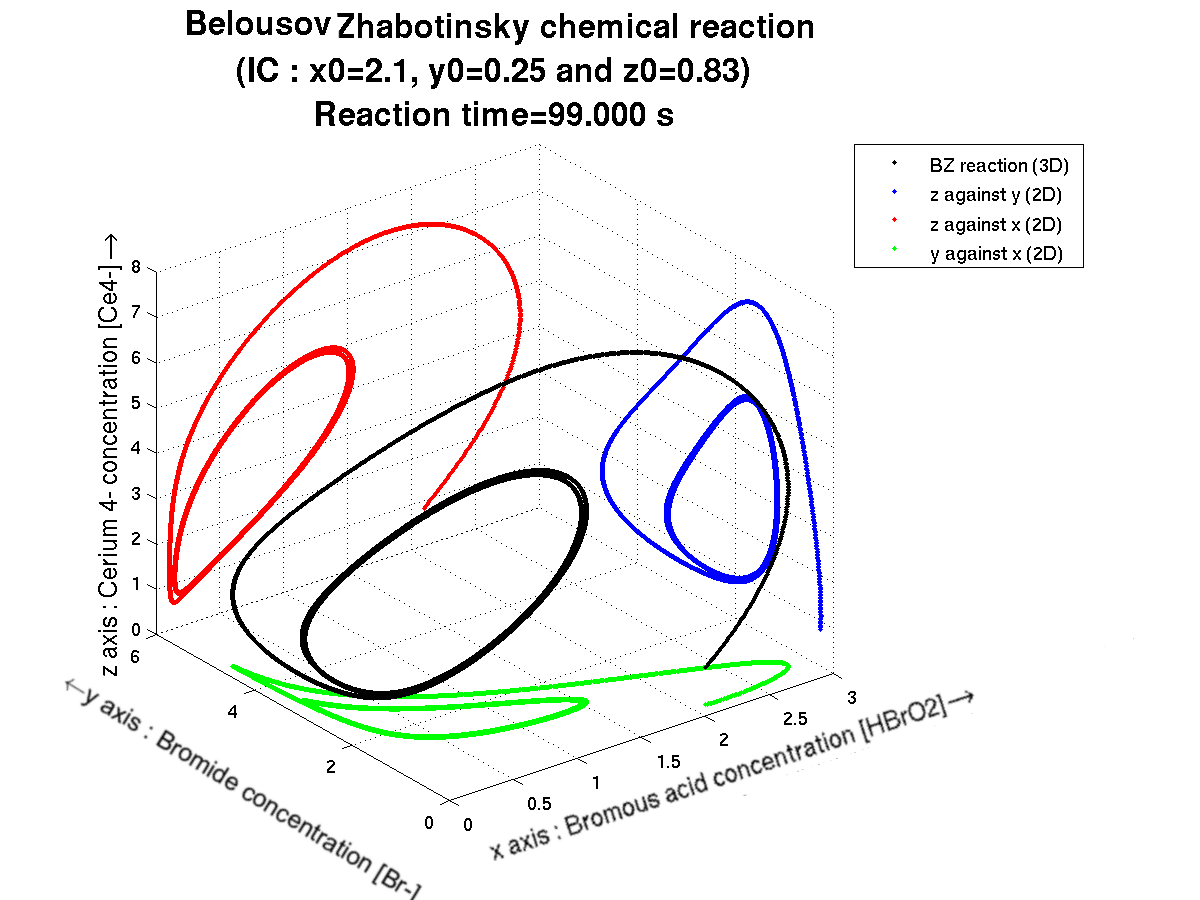
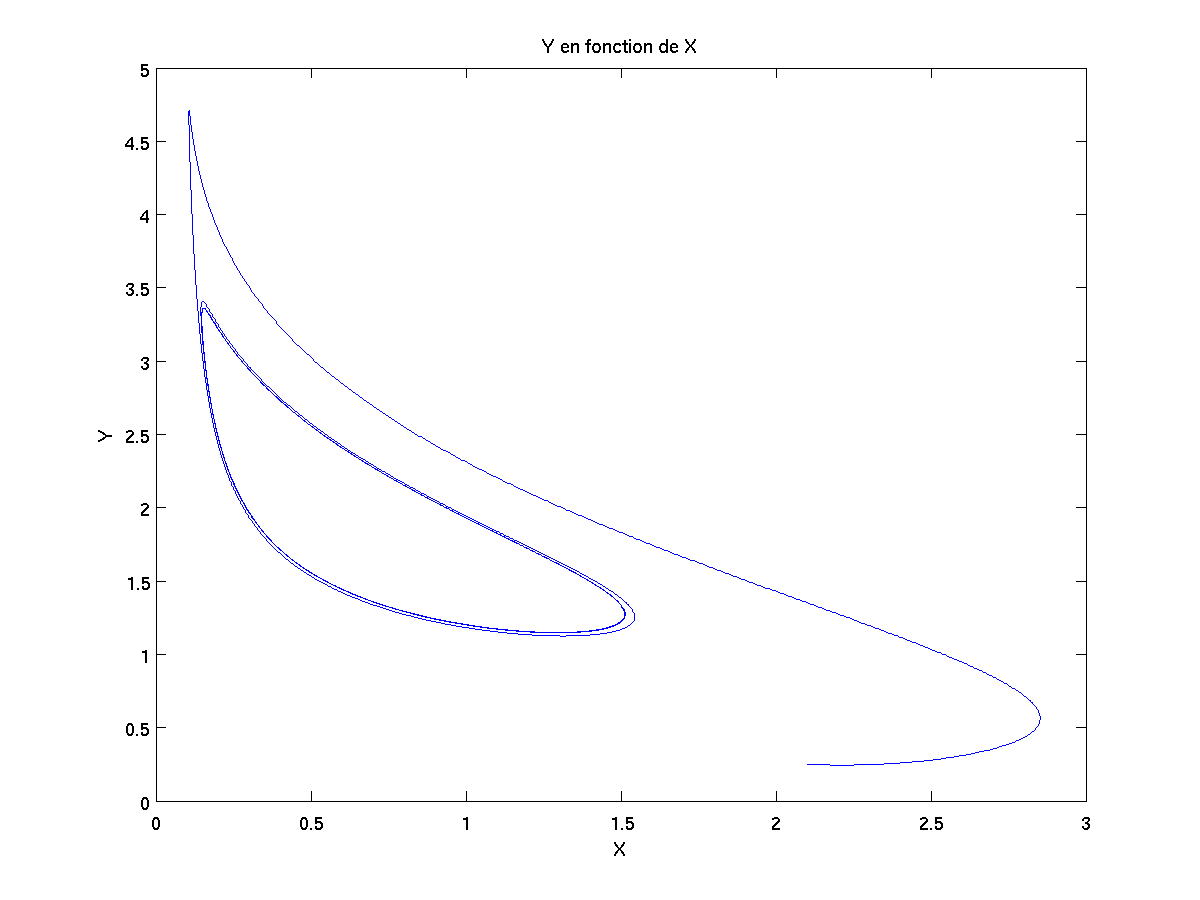
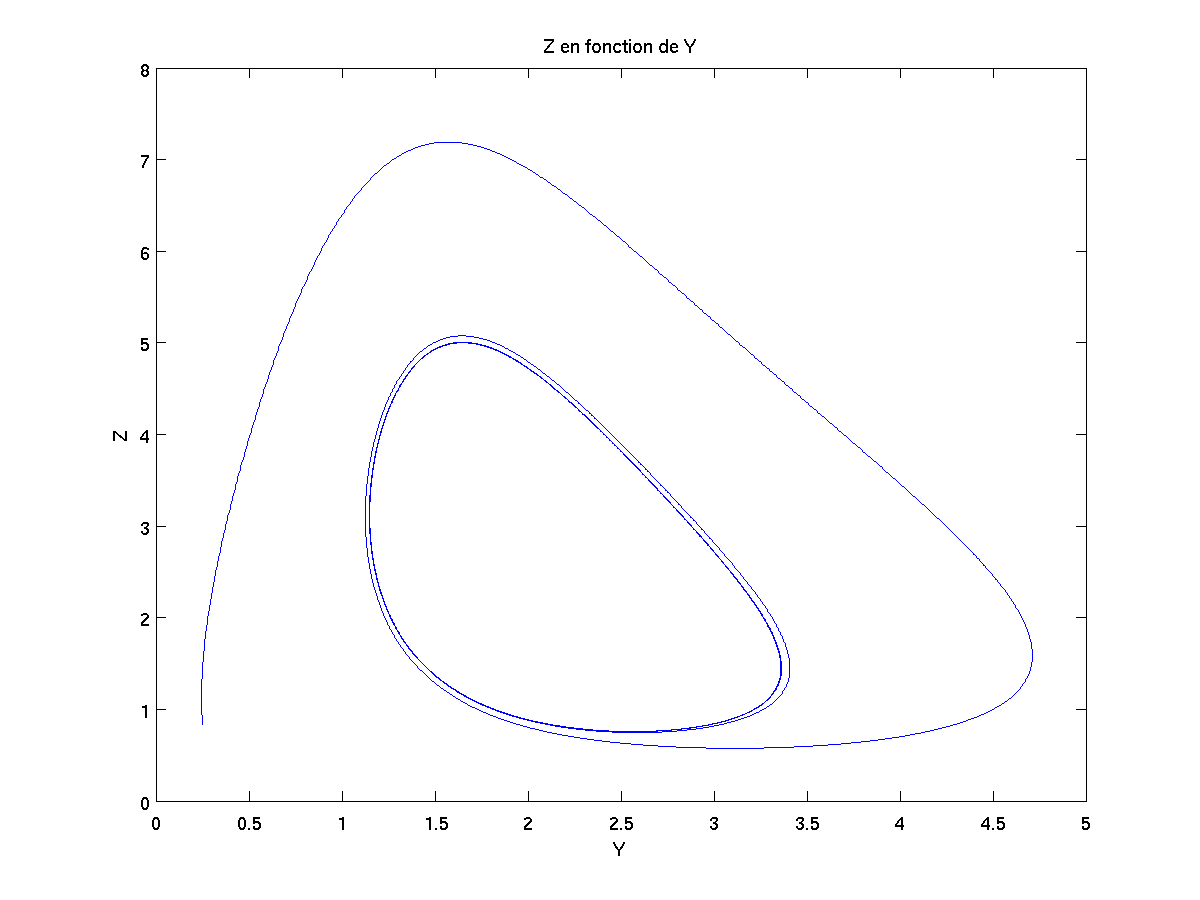
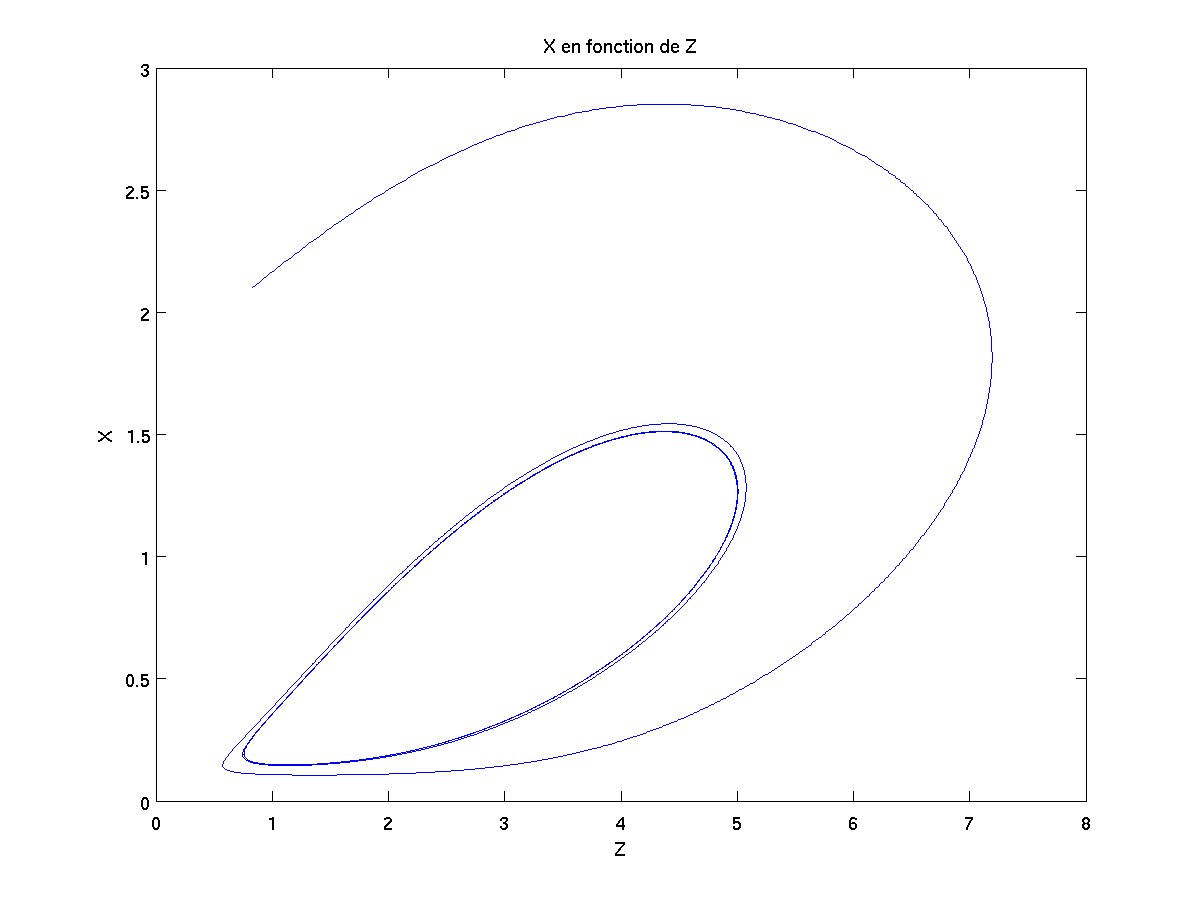
Si on trace les résultats X={x(t),t dans I}, Y={y(t),t dans I} et Z={z(t),t dans I} au cours du temps, on obtient alors la courbe noire ci-dessous. Si en plus on veut projeter cette courbe sur chaque face du cube en arrière-plan, on obtient alors les courbes vertes, bleues et rouges ci-dessous.
ATTENTION : la couleur des courbes de projection n'a rien avoir avec la couleur de la solution !
La réaction commence au bout de la courbe noire. Puis au fur et à mesure du temps, la réaction oscillante se met en place : il apparait alors les cycles sur chacun des plans.
Voici les courbes issues de la projection de la courbe noire sur la box en arrière-plan :
Expérimentalement, on observe un changement de couleur au fur et à mesure de la réaction chimique car les ions non spectateurs sont pris dans ces cycles (2D) et ils ne peuvent s'y en échapper.
De temps à autre la concentration d'un ion prédomine par rapport aux autres car différentes molécules se forment et se défont suivant la concentration en ions x,y et z. au cours du temps;
==> la solution se colore.
A certains moments de la réaction la solution parait incolore car les ions se lient entre-eux pour former des molécules "incolores" !
Voilà en gros pour l'explication de cette réaction oscillante à l'aide d'un modèle numérique.
PS : Je suis sûr que ce que je raconte à propos des ions et des molécules n'est pas exact, mais c'est simplement pour comprendre le principe.
Dans cette dernière partie, nous allons compiler tout ce que nous avons fait pour résoudre ce système d'ED couplées pour tracer le modèle numérique 3D associé à la réaction de BZ . Le voici justement en exclusivité :
E) Animation de la réaction de B-Z en 3D :
E.1) Animation rapide :
E.2) Animation lente :
C'est joli à voir je trouve, mais c'est mieux de comprendre à quoi cette animation sert ^^
La réaction de BZ se poursuit sur une période I=[0;100] pour des concentrations initiales (en mol.L^-1) en espèces non spectatrices : x(t=0)=2.1, y(t=0)=0.25 et z(t=0)=0.83
On peut voir alors la réaction (courbe en noire) qui progresse et les projections associées (courbes colorées) au cours du temps.
Conclusion
J'espère vous avoir appris des nouveautés concernant cette réaction et d'avoir été à peu près clair... Vous pouvez constater que les modèles numériques apportent beaucoup pour la compréhension de cette réaction oscillante.
A retenir : un modèle vaut mieux que 1000 mots !
Si un jour vous voulez tester expérimentalement cette réaction, souvenez-vous qu'il faudra préparer en avance les bonnes concentrations initiales en chaque réactifs afin que l'oscillation se fasse correctement : ce genre d'expérience demande une grande préparation en amont.
A vous de jouer maintenant !
Ouverture
La chose que je ne vous ai pas dit est que le système d'ED que je vous ais présenté peut aussi s'apparenter à la dynamique des populations (du type Lotka-Volterra (2D) avec un terme supplémentaire lié à la quantité de nourriture).
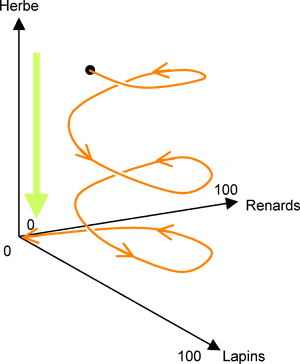
Un super article fait le lien entre ces deux notions :
Pour aller plus loin
Les motifs chimiques : http://www.di.ens.fr/~granboul/enseignement/formes/reactionsoscillantes/belousov.html
La cinétique chimique : http://uel.unisciel.fr/chimie/cinet/cinet/co/cinet.html
Ordre de réaction : https://fr.wikipedia.org/wiki/Ordre_de_réaction
Turing et la morphogénèse :
http://www.lptmc.jussieu.fr/user/lesne/Turing-preprint.pdf
https://media4.obspm.fr/public/M2R/appliquettes/Turing/AutomateTuring_website.html
 A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?