A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
La morphogénèse
Définition
La théorie de la morphogénèse chimique
Tout phénomène physico-chimique impliquant diffusion (ou transport) et réactions chimiques peut être décrit par un modèle de réaction-diffusion. Lorsqu'ils sont maintenus loin d'un équilibre thermodynamique, certains systèmes couplant réaction et diffusion de fluides ont la capacité de produire des variations spatiales de concentrations sous la forme de motifs qui présentent un haut niveau d'organisation. Comparés aux textures rencontrées dans la nature, ces motifs montrent un degré de réalisme rarement atteint avec d'autres catégories de modèles.
En 1952, dans les fondements d'une théorie de la morphogénèse chimique, Alan Turing a ainsi émis l'hypothèse qu'un mécanisme de réaction-diffusion est réellement à l'origine des structures présentes dans certains tissus biologiques - une chimie du vivant en quelque sorte. Si une telle hypothèse n'a jamais pu être démontrée, elle reste d'actualité alors que, dans ce domaine, les simulations informatiques conservent une large avance sur les expérimentations en laboratoire. En construisant un modèle mathématique simple à base d'équations aux dérivées partielles, Turing est parvenu à reproduire les structures qu'il observait.
http://math.univ-lyon1.fr/~pujo/TURING-IXXI.pdf
Son idée qui paraissait complètement contre intuitive, à savoir, comment un équilibre qui est localement asymptotiquement stable peut se déstabiliser en ajoutant de la diffusion, qui par essence
tant à lisser toutes les bosses. C’est justement la combinaison de la réaction et de la diffusion qui permet de faire émerger des formes. L’intuition de Turing, combinée à celle de Fourier
établie 145 ans plus tôt, a permis d’ouvrir la voie vers un domaine qui a explosé à partir des années 70.
Illustration de la théorie de la morphogénèse chimique
<<Normalement, nous pensons à la diffusion comme un processus qui lisse les choses. Pensez à une distribution de densité inégale dans un gaz. Alors que les atomes se diffusent, la densité devient uniforme. Lorsque vous avez de la diffusion avec des réactions chimiques non linéaires se produisant, c’est le contraire qui se passe . Les différents types chimiques se séparent et forment des domaines composition chimique distincts. Cela a été la surprenante découverte d’Alan Turing.>> Nigel Goldenfeld
http://www.lecactusheuristique.com/article-auto-organisation-et-motifs-biologiques-38585774.html
Deux morphogènes (dont la nature importe peu) diffusent, en interaction l’un avec l’autre, en surface d’un milieu vivant homogène :
- un activateur A qui favorise sa propre formation et qui diffuse lentement
- un inhibiteur B dont la formation est stimulée par A, qui diffuse rapidement et qui freine la formation de A
Application pratique
Motifs sur les pelages des animaux
Mélanine
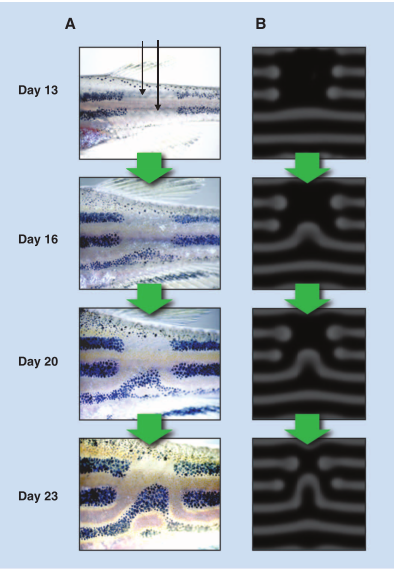
Formation des dents
Il est probable que
la génération des dents pourrait être gérée par la diffusion-réaction de morphogènes le long de la mâchoire, soit un problème de Turing à une dimension. Lorsque la mâchoire de l'embryon grandit,
la période spatiale des structures de Turing restant constante, de nouveaux pics apparaissent entre les précedents. Chez les alligators, si l'on numérote les dents en partant du devant de la
mâchoire, on observe que les dents poussent dans l'ordre bien précis 1,3,5,7,9... puis 2,4,6,8,10... soit une première série, puis une seconde entre les précédentes.
Les tâches de l'ange de mer impérial juvénile
http://www.uoguelph.ca/~mgarvie/turing.html
On voit bien que la tâche s'est propagée lors de la formation du poisson.
On retrouve ici le phénomène de propagation annoncé par Turing.
La différence corps/queue chez le guepard
Un résultat célèbre obtenu par Alan TURING alors qu'il étudiait la morphégénèse.
Avec son modèle, TURING parvint à expliquer pourquoi, alors que les mêmes mécanismes cellulaires locaux étaient à l'oeuvre sur l'ensemble du corps d'un animal comme le guépard, ce dernier présentait des taches circulaires sur le corps et des bandes orthogonales à la direction privilégiée sur la queue (cf figure ci-dessus).
Bien que le mécanisme local d'activation des cellules reste le même, tout se passe comme si l'évolution des motifs dépendait de la géométrie globale du système! En effet, les mémes paramètres vont donner des bandes en géométrie queue et des taches en géométrie corps.
L'explication réside dans les conditions aux limites imposées au système. Ici, le terme queue est abusif en ce sens que, si la géométrie corps modélise bel et bien une sphère ( ~ corps réel de guépard ou de dalmatien), la géométrie queue correspond en fait à un tore (conditions au limites verticales mais aussi horizontales - le début et la fin de la queue sont reliés! ).
La formation des dunes de sable
Certains géophysiciens ont appliqué le modèle de Turing avec succès à la formation de dunes.
On retrouve les motifs que l'on peut générer informatiquement grâce à la théorie de Turing; il y a donc forcément un lien.
Les équations de Navier-Stokes expriment bien une propagation de l'air en tant que fluide , avec certains frottements de viscosité qui pourrait expliquer la présence de tels motifs.
