A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
La fonction Gamma d'Euler
Définition
Pour tout nombre complexe de partie réelle strictement positive, on défini la fonction Gamma par :
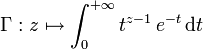
Graphe
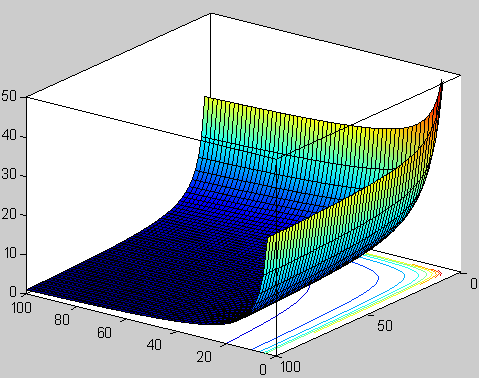
Le long de l'axe des réels
Dans le plan complexe
La fonction Gamma interpole la fonction factorielle
Dérivabilité de la fonction Gamma
La fonction gamma est indéfiniment dérivable sur R+*, et on a l'égalité :
Valeurs remarquables
Formule asymptotique de Stirling
On connait la formule de Stirling pour la factorielle :
Et bien elle est encore valable pour la fonction Gamma (sous certaines conditions !) :
Fonction bêta
Lien entre la fonction Gamma et la fonction Bêta
