A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
Les Octonions (8D)
Présentation et historique des Octonions
Qu'est-ce-qu'un Octonion ?
En mathématiques, les Octonions ou Octaves sont une extension non-associative des quaternions. Ces octonions constituent une algèbre à 8 dimensions sur les réels.
Cette algèbre est notée :
Comme il ne présente pas la propriété d'associativité, les Octonions ont connu moins de succès que les Quaternions.
Historique d'apparition
En 1843, John T.Graves un proche de sir William Hamilton, découvre les Octonions, appelés alors Octaves.
Voici une lettre écrire par Hamilton à Graves
Les Octaves furent également découverts en parallèle par Arthur Cayley.
C'est pourquoi les Quaternions sont aussi appelés Octaves de Cayley ou algèbre de Cayley.
Définition
Un Octonion admet comme base (1, i, j, k, l, il, jl, kl) et s'écrit :
Les coefficiants e_n sont des réels.
Le conjugué d'un Octonion
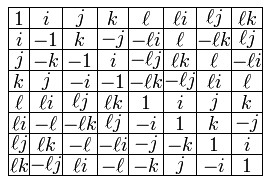
Table de multiplication des Octonions
On remarque que la table de multiplication n'est pas symétrique, d'où la non commutativité de la multiplication des Octonions.
On forme ainsi l'égalité suivante :
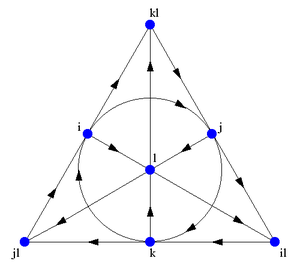
Plan mnémotechnique de Fano pour les multiplications entre unitaires
Utilité des Octonions
Les octonions sont utilisés pour les généralisations non-associative de la mécanique quantique. Par exemple, l'équation de mouvement de Heisenberg est modifié en utilisant un opérateur commutatif et non-associatif.
Pour aller plus loin avec les Octonions
"Images" d'Octonions
Découvrons à présent l'ensemble des Octonions Fendus.
Pour cela, cliquez ICI.
