A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
Les Quaternions
Historique des Quaternions
Les quaternions furent « découverts » par William Rowan Hamilton en 1843 à partir des travaux de Leonhard Euler et, au siècle suivant, Carl Friedrich Gauss. Il étudiait alors
l'interprétation géométrique de l'arithmétique de nombres complexes dans le plan et cherchait à obtenir des résultats analogues dans l'espace à trois dimensions.
Après des années de recherches sur la construction d'une algèbre avec des « triplets » de trois nombres réels, il butait sur la multiplication, et en particulier la conservation des normes (Georg
Ferdinand Frobenius a démontré en 1877 qu'une telle multiplication de triplets était impossible à définir).
Hamilton eut alors l'idée d'utiliser des « quadruplets » en employant une dimension supplémentaire. Selon ses dires, il marchait, le 16 octobre 1843, le long du canal royal, avec son
épouse quand soudain lui vint à l'esprit la solution sous la forme des relations : i^2 = j^2 = k^2 = i.j.k = (–1).
Cela impliquait l'insertion d'une 4e composante aux triplets. Avec des quadruplets il pouvait effectuer des multiplications mais il dut abandonner la commutativité. C'est de là que vient le nom des quaternions.
Il grava alors promptement ces relations avec un couteau dans une pierre du pont de Brougham (maintenant appelé Broom Bridge) à Dublin. Cette inscription, malheureusement effacée par le temps, a été remplacée par une plaque à la mémoire de Sir William Rowan Hamilton.
La théorie a été généralisée et d'autres ensembles comme les octonions ont été découverts par la suite. Un élément d'un ensemble de cette nature fut qualifié de nombre hypercomplexe jusqu'à la Première Guerre mondiale. Ces ensembles sont maintenant considérés comme des exemples d'algèbres semi-simples. Le théorème d'Artin-Wedderburn fournit une méthode de construction générique et se fonde sur la théorie des représentations d'un groupe fini. La construction des quaternions est donnée dans l'article représentations du groupe des quaternions. Elle correspond à l'unique algèbre simple fidèle de la représentation du groupe des quaternions sur le corps des nombres réels.
Ironiquement, Frobenius démontra en 1877, après la mort de Hamilton que la multiplication de triplets est impossible.
La biographie d'Hamilton est exposée ICI.
Définitions
On note H l'ensemble des Quaternions (H en référence à Hypercomplexe ou à Hamilton)
Tout quaternion H se note de la manière suivante :
1, i, j et k sont les quatre unitaires obéissant au tableau de multiplication suivant :
a s'appelle la composante réelle (ou scalaire) de H, tandis que b, c et d sont les composantes complexes de H.
On dit aussi que a est le scalaire de H et que le triplet {b, c, d} ou [b.i + c.j + d.k] est le vecteur de H (ou sa partie vectorielle).
Propriétés des Quaternions
La non-commutativité partielle des Quaternions
Deux nombres "a" et "b" sont commutatifs si le produit de a avec b est égal au produit de b avec a.
Les Quaternions sont partiellement commutatifs; en effet, si on regarde le tableau de multiplication réalisé précédemment, on remarque que certaines unitaires sont communtatives et d'autres pas :
Exemple de la commutativité
Exemple de la non commutativité
On peut donc retenir :
- un unitaire multiplié par un autre unitaire est non-commutatif.
- un unitaire multiplié par lui-même ou par une unitaire réelle est commutatif.
L'histoire de la commutativité peut être illustrer avec deux rotations successives d'un cube coloré.
Le patron de ce cube est le suivant :
On va ensuite orienter ce cube :
Puis, nous allons réaliser deux rotations (dans le sens trigonométrique chacune) successives de 90° :
- Autour de X
2. Autour de Y
Réalisons maintenant de même procédé mais en commençant par la rotation autour de Y :
1. Autour de Y
2. Autour de X
Les 2 cubes obtenus sont différents. L'ordre de rotation influe ainsi sur le résultat final.
Cet exemple montre la non commutativité des cubes.
Et bien c'est la même chose pour les Quaternions !
La somme de Quaternions
Soient deux Quaternions Q1 et Q2 défini par :
La somme de Q1 avec Q2 s'écrit alors :
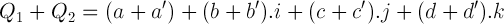
La somme de deux Quaternions est donc commutative et associative.
Animation de l'addition des quaternions
http://www.alcys.com/p5/Alcys_Quat_addition/applet/index.html
Le conjugué d'un Quaternion
La norme d'un Quaternion
Lorsque la norme d'un quaternion vaut 1 on dit que le quaternion est normalisé. C'est cette catégorie de quaternions qui va nous intéresser pour la 3D.
Le produit de Quaternions
On développe CORRECTEMENT (pas dans l'importe quel sens ET sans faire de commutativité) :
On rassemble les parties réelles entre-elles et on simplifie les produits des unitaires (grâce aux tableau de multiplication précédent) :
On regroupe les composantes d'un même unitaire entre-elles :
Les Quaternions sont-ils utiles ?
Généralités
La théorie des quaternions introduite au milieu du 19e siècle, trouvait de nombreuses applications dans la mécanique quantique, la mécanique classique et la théorie de la relativité. Les quaternions furent utilisés plus tard dans les applications liés à l'aérospatial, et dans les simulateurs de vol.
Cependant ce n'est que dans un passé récent que les graphistes et programmateurs de jeux découvrirent le vrai potentiel des quaternions et commencèrent à les utiliser pour décrire des
rotations autour d'un axe arbitraire.
Des graphismes d'ordinateur, le domaine d'application des quaternions s'étendit rapidement dans les champs de la visualisation, des fractales et de la réalité virtuelle.
Intérêt pour la rotation
Les quaternions sont très utiles dans les domaines de l'informatique, de la vision robotique, des graphismes et de l'animation.
L'intérêt d'utiliser les quaternions plutôt que d'autres représentations comme les angles d'Euler provient du fait que les quaternions permettent de s'approcher au plus près des solutions
de systèmes algébriques intégrant des paramètres de rotation inconnus.
Les graphistes ont maintenant réalisés le potentiel des quaternions en tant que puissant et très général opérateur de rotation.
Ils sont utilisés dans l'algorithme avancé dans la programmation de jeux et dans l'animation comme la simulation de mouvement de caméra dans un espace en trois dimensions.
Au lieu de tourner un objet via une série de rotations successives, les quaternions permettent au programmeur de tourner un objet autour d'un axe arbitraire et d'un angle quelconque. La rotation
est néanmoins toujours réalisée par des calculs matriciels. Cependant, au lieu de multiplier les matrices ensemble, il suffit de multiplier les quaternions les représentant. Le résultat final est
reconverti en la matrice désirée.
Les quaternions offrent aussi l'avantage de permettre l'interpolation. Ceci permet des rotations plus souples et plus réalistes.
Voici une vidéo explicative (en anglais) sur les quaternions
Calculette de Quaternions
Se documenter sur les Quaternions
http://meca.cannes-aero-patrimoine.net/mecaspa/SCAO/QUATERN/QUATERN0.HTM
http://villemin.gerard.free.fr/Wwwgvmm/Type/ImagQuat.htm
http://fr.wikipedia.org/wiki/Quaternions_et_rotation_dans_l'espace
Pourquoi les Quaternions sont-ils dans la 4D et non dans la 3D ?
http://math.stackexchange.com/questions/72012/why-is-quaternion-algebra-4d-and-not-3d
http://www.siteduzero.com/forum/sujet/nombres-complexes-84249
